Office Applications and Entertainment, Magic Cubes

8a   Perfect Concentric Magic Cubes (6 x 6 x 6)
     Center Cubes

8a-1 Lemma

Order 4 Almost Perfect Magic Cubes are not suitable for the construction of order 6 Perfect Concentric Magic Cubes.

8a-2 Proof

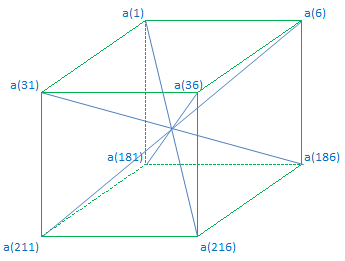
The application of order 4 Almost Perfect Magic Cubes as center cubes for order 6 Perfect Concentric Magic Cubes would require a border with corner pairs which are non symmetrical over the space diagonals, say:

   a( 1) + a(216)+ d(1) = s6
   a( 6) + a(211)+ d(2) = s6
   a(31) + a(186)+ d(3) = s6
   a(36) + a(181)+ d(4) = s6

Based on the above the defining equations of the edge of an order 6 Perfect Concentric Magic Cube can - after deduction - be written as:

a(  5) =       a(212) + a(213) + a(214) - a(6)   - a(1)
a( 25) =       a(192) + a(198) + a(204) - a(31)  - a(1)
a( 30) =       a(187) + a(193) + a(199) - a(36)  - a(6)
a( 35) =  s6 - a(185) - a(36)  - a(31)  - a(181) - a(186)
a( 67) =  s6 - a(103) - a(139) - a(175) - a(31)  - a(211)
a( 72) =  s6 - a(108) - a(144) - a(180) - a(36)  - a(216)
a(145) =  s6 - a(180) - a(36)  - a(1)   - a(181) - a(216)
a(150) =  s6 - a(175) - a(31)  - a(6)   - a(186) - a(211)
a(182) =  s6 - a(183) - a(184) - a(185) - a(181) - a(186)
a(187) =  s6 - a(193) - a(199) - a(205) - a(181) - a(211)
a(192) =  s6 - a(198) - a(204) - a(210) - a(186) - a(216)
a(212) =  s6 - a(213) - a(214) - a(215) - a(211) - a(216)

a(36)  =    s6   - a(181) - d(4)
a(31)  = -  s6/3 - a(186) + d(4)
a(6)   =    s6   - a(211) - d(4)
a(1)   = -  s6/3 - a(216) + d(4)
d(1)   =  4*s6/3 - d(4)
d(2)   =           d(4)
d(3)   =  4*s6/3 - d(4)
d(4)   =  2*s6/3

a(2) = s6/3 - a(212)
a(3) = s6/3 - a(213)
a(4) = s6/3 - a(214)
a(7) = s6/3 - a(192)

a(12) = s6/3 - a(187)
a(13) = s6/3 - a(198)
a(18) = s6/3 - a(193)
a(19) = s6/3 - a(204)
a(24) = s6/3 - a(199)

a(32) = s6/3 - a(182)
a(33) = s6/3 - a(183)
a(34) = s6/3 - a(184)
a(37) = s6/3 - a(72)

a( 42) = s6/3 - a(67)
a( 73) = s6/3 - a(108)
a( 78) = s6/3 - a(103)
a(109) = s6/3 - a(144)
a(114) = s6/3 - a(139)

which proofs that the space diagonals d(1), d(2), d(3) and d(4) of the order 4 center cube should be identical.

Consequently order 4 Almost Perfect Cubes are not suitable as center cubes for order 6 Perfect Concentric Magic Cubes (q.e.d.).