Magic Cubes (6h)

Office Applications and Entertainment, Magic Cubes
	Index	About the Author

4.9 Pantriagonal Magic Cubes, Moriyama (5 x 5 x 5)

4.9.1 Introduction

The cube shown below is a Pantriagonal Magic Cube of the 5^th order, published by Yoshio Moriyama in 1967, with the additional property that the diagonals of the centerplanes sum to the Magic Sum.

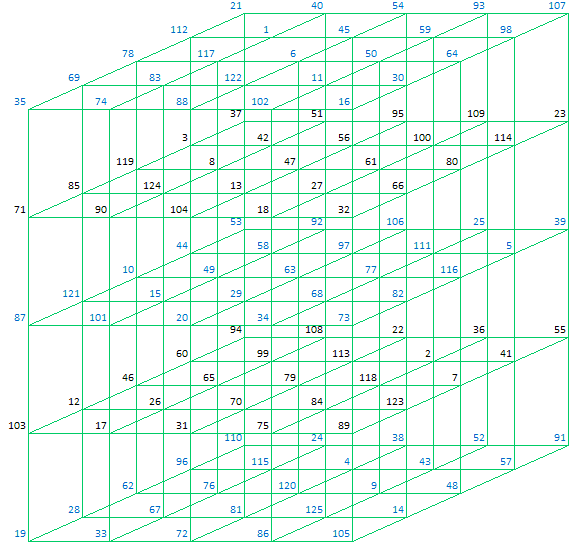
Plane 11 (Top)

21	40	54	93	107
112	1	45	59	98
78	117	6	50	64
69	83	122	11	30
35	74	88	102	16

Plane 12

37	51	95	109	23
3	42	56	100	114
119	8	47	61	80
85	124	13	27	66
71	90	104	18	32

Plane 13

53	92	106	25	39
44	58	97	111	5
10	49	63	77	116
121	15	29	68	82
87	101	20	34	73

Plane 14

94	108	22	36	55
60	99	113	2	41
46	65	79	118	7
12	26	70	84	123
103	17	31	75	89

Plane 15

110	24	38	52	91
96	115	4	43	57
62	76	120	9	48
28	67	81	125	14
19	33	72	86	105

Due to the center planes property the cube is only member of a Class of 48 elements which can be obtained by rotation / reflection.

The Class of 48 elements which can be obtained by rotation / reflection of this Pantriagonal Cube is shown in Attachment 4.9.1.

4.9.2 Analytic Solution (1)

In general Magic Cubes of order 5 can be represented as follows:

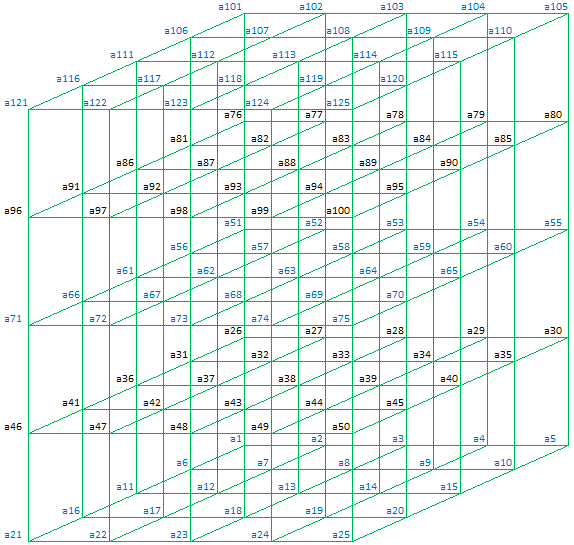
Plane 11 (Top)

a101	a102	a103	a104	a105
a106	a107	a108	a109	a110
a111	a112	a113	a114	a115
a116	a117	a118	a119	a120
a121	a122	a123	a124	a125

Plane 12

a76	a77	a78	a79	a80
a81	a82	a83	a84	a85
a86	a87	a88	a89	a90
a91	a92	a93	a94	a95
a96	a97	a98	a99	a100

Plane 13

a51	a52	a53	a54	a55
a56	a57	a58	a59	a60
a61	a62	a63	a64	a65
a66	a67	a68	a69	a70
a71	a72	a73	a74	a75

Plane 14

a26	a27	a28	a29	a30
a31	a32	a33	a34	a35
a36	a37	a38	a39	a40
a41	a42	a43	a44	a45
a46	a47	a48	a49	a50

Plane 15

a1	a2	a3	a4	a5
a6	a7	a8	a9	a10
a11	a12	a13	a14	a15
a16	a17	a18	a19	a20
a21	a22	a23	a24	a25

The equations for a Moriyama Pantriagonal Magic Cube of the fifth order can be summarised as follows:

The Rows (25), Columns (25) and Pillars (25) sum to the Magic Sum (315);
All pantriagonals (100) sum to the Magic Sum (315);
All diagonals of the center planes (6) sum to the Magic Sum (315).

After deduction of the defining equations (181), the following set of linear equations - describing the Moriyama Pantriagonal Magic Cubes of the 5^th order - can be obtained:

a(121)=315-a(122)-a(123)-a(124)-a(125)
a(116)=315-a(117)-a(118)-a(119)-a(120)
a(115)=315-a(117)-a(118)-a(120)-a(125)
a(114)=+a(118)+a(120)-a(124)
a(113)=+a(117)+a(119)-a(123)
a(112)=315-a(117)-a(119)-a(120)-a(122)
a(111)=-315+a(117)+a(120)+a(122)+a(123)+a(124)+a(125)
a(110)=-315+a(117)+a(118)+a(120)+a(122)+a(123)+a(125)
a(109)=315-a(118)-a(120)-a(123)-a(125)
a(108)=315-a(117)-a(119)-a(122)-a(124)
a(107)=-315+a(117)+a(119)+a(120)+a(122)+a(124)+a(125)
a(106)=315-a(117)-a(120)-a(122)-a(125)
a(105)=315-a(120)-a(122)-a(123)-a(125)
a(104)=-a(119)+a(123)+a(125)
a(103)=-a(118)+a(122)+a(124)
a(102)=315-a(117)-a(122)-a(124)-a(125)
a(101)=-315+a(117)+a(118)+a(119)+a(120)+a(122)+a(125)
a(97)=(-a(98)+a(99)-2*a(100)+3*a(117)+a(118)-a(119)+2*a(120))/3
a(96)=(945-2*a(98)-4*a(99)-a(100)-3*a(117)-a(118)+a(119)-2*a(120))/3
a(94)=(-1323+a(95)+a(99)+2*a(100)+3*a(117)+a(118)+4*a(120)+4*a(122)+a(123)+3*a(124)+3*a(125))/2
a(93)=(-189-2*a(98)+2*a(99)-a(100)+3*a(117)-a(118)+a(119)+a(120)+3*a(122)-3*a(123)+3*a(124))/3
a(92)=(5103-3*a(95)-2*a(98)-7*a(99)-4*a(100)-15*a(117)-7*a(118)-2*a(119)-14*a(120)-6*a(122)-3*a(123)-3*a(124)-9*a(125))/6
a(91)=189-a(95)+a(98)+a(118)-2*a(122)+a(123)-2*a(124)
a(90)=(-945-a(95)+2*a(98)+a(99)+3*a(117)+3*a(118)+4*a(120)+3*a(123)-a(124)+3*a(125))/2
a(89)=(-189+3*a(95)-2*a(98)-a(99)-a(100)+3*a(117)-a(118)+a(119)+a(120)+3*a(122)-3*a(123)+3*a(124))/3
a(88)=(567-4*a(98)-2*a(99)+a(100)-3*a(117)-2*a(118)-a(119)-a(120)+3*a(122)+3*a(124))/3
a(87)=(378-3*a(95)+2*a(98)+a(99)+a(100)+a(118)+2*a(119)-a(120)-3*a(122)-3*a(124))/3
a(86)=(3213+3*a(95)+2*a(98)+a(99)-2*a(100)-9*a(117)-5*a(118)-4*a(119)-10*a(120)-6*a(122)-3*a(123)-3*a(124)-9*a(125))/6
a(85)=(2835+3*a(95)-2*a(98)-a(99)-4*a(100)-3*a(117)-7*a(118)-2*a(119)-8*a(120)-9*a(123)+3*a(124)-9*a(125))/6
a(84)=(1134-3*a(95)-a(98)-2*a(99)-2*a(100)-3*a(117)+a(118)-a(119)-a(120)-3*a(122)+3*a(123)-3*a(124))/3
a(83)=(378+2*a(98)-2*a(99)+a(100)+a(118)+2*a(119)-a(120)-3*a(122)-3*a(124))/3
a(82)=(-378+3*a(95)-2*a(98)+2*a(99)+2*a(100)-a(118)-2*a(119)+a(120)+3*a(122)+3*a(124))/3
a(81)=(-3213-3*a(95)+4*a(98)+5*a(99)+2*a(100)+9*a(117)+5*a(118)+4*a(119)+10*a(120)+6*a(122)+3*a(123)+3*a(124)+9*a(125))/6
a(80)=(945-3*a(95)-2*a(98)-a(99)-a(100)-3*a(117)-a(118)+a(119)-2*a(120))/3
a(79)=(1323-a(95)+2*a(98)-a(99)-3*a(117)-a(118)-4*a(120)-4*a(122)-a(123)-3*a(124)-3*a(125))/2
a(78)=(189+a(98)+2*a(99)-a(100)+2*a(118)-2*a(119)+a(120)-3*a(122)+3*a(123)-3*a(124))/3
a(77)=(-3213+3*a(95)+4*a(98)-a(99)+2*a(100)+9*a(117)+5*a(118)+4*a(119)+10*a(120)+6*a(122)+3*a(123)+3*a(124)+9*a(125))/6
a(76)=(-567+3*a(95)-4*a(98)+a(99)+a(100)+3*a(117)-2*a(118)-a(119)+2*a(120)+6*a(122)-3*a(123)+6*a(124))/3
a(75)=(945-2*a(98)-a(99)-a(100)-3*a(117)-a(118)+a(119)-2*a(120)-3*a(125))/3
a(74)=+a(98)+a(100)-a(124)
a(73)=(-a(98)+4*a(99)-2*a(100)+3*a(117)+a(118)-a(119)+2*a(120)-3*a(123))/3
a(72)=(945+a(98)-4*a(99)-a(100)-3*a(117)-a(118)+a(119)-2*a(120)-3*a(122))/3
a(71)=(-945-a(98)+a(99)+a(100)+3*a(117)+a(118)-a(119)+2*a(120)+3*a(122)+3*a(123)+3*a(124)+3*a(125))/3
a(70)=(-945-a(95)+2*a(98)+a(99)+2*a(100)+3*a(117)+3*a(118)+2*a(120)+3*a(123)-a(124)+3*a(125))/2
a(69)=(-189+3*a(95)-2*a(98)+2*a(99)-a(100)+3*a(117)-a(118)-2*a(119)+a(120)+3*a(122)-3*a(123)+3*a(124))/3
a(68)=(567-a(98)-2*a(99)+a(100)-3*a(117)-5*a(118)-a(119)-a(120)+3*a(122)+3*a(124))/3
a(67)=(378-3*a(95)+a(98)+2*a(99)-a(100)+2*a(118)+a(119)+a(120)-3*a(122)-3*a(124))/3
a(66)=(3213+3*a(95)-2*a(98)-7*a(99)-4*a(100)-9*a(117)-a(118)+4*a(119)-8*a(120)-6*a(122)-3*a(123)-3*a(124)-9*a(125))/6
a(65)=(945+9*a(95)-2*a(98)-a(99)-4*a(100)+3*a(117)-a(118)-2*a(119)-2*a(120)-9*a(123)+3*a(124)-3*a(125))/6
a(64)=(-1701-3*a(95)-2*a(98)-a(99)+2*a(100)+3*a(117)-a(118)-2*a(119)+4*a(120)+6*a(122)+9*a(123)+9*a(124)+9*a(125))/6
a(63)=63
a(62)=(819+a(95)-2*a(98)-a(99)-3*a(117)-3*a(118)-2*a(120)+2*a(122)-a(123)+a(124)-3*a(125))/2
a(61)=(-189-9*a(95)+10*a(98)+5*a(99)+2*a(100)+3*a(117)+11*a(118)+4*a(119)+4*a(120)-12*a(122)+3*a(123)-15*a(124)+3*a(125))/6
a(60)=(945-9*a(95)+2*a(98)+a(99)-2*a(100)-3*a(117)+a(118)+2*a(119)+2*a(120)-6*a(122)+3*a(123)-3*a(124)+3*a(125))/6
a(59)=(1701+3*a(95)+2*a(98)-5*a(99)-2*a(100)-3*a(117)+a(118)+2*a(119)-4*a(120)-6*a(122)-3*a(123)-3*a(124)-3*a(125))/6
a(58)=-63-a(98)+a(122)+a(123)+a(124)
a(57)=(-567-3*a(95)+8*a(98)+a(99)+4*a(100)+3*a(117)+7*a(118)+2*a(119)+2*a(120)-6*a(122)+3*a(123)-9*a(124)+3*a(125))/6
a(56)=(63+3*a(95)-2*a(98)+a(99)+a(117)-3*a(118)-2*a(119)+4*a(122)-3*a(123)+3*a(124)-a(125))/2
a(55)=(945+3*a(95)-2*a(98)-a(99)+2*a(100)-3*a(117)-7*a(118)-2*a(119)-2*a(120)+6*a(122)-3*a(123)+3*a(124)-3*a(125))/6
a(54)=(1134-3*a(95)-a(98)+a(99)-2*a(100)-3*a(117)+a(118)+2*a(119)-a(120)-3*a(122)-3*a(124)-3*a(125))/3
a(53)=(378+5*a(98)-2*a(99)+a(100)+4*a(118)+2*a(119)-a(120)-6*a(122)-6*a(124))/3
a(52)=-441+a(95)-a(98)+a(99)+2*a(117)-a(119)+a(120)+2*a(122)+2*a(124)+a(125)
a(51)=(189-a(95)-a(99)-a(117)-a(118)+a(123)+a(124)+a(125))/2
a(50)=(-945+2*a(98)+a(99)+a(100)+3*a(117)+a(118)-a(119)+2*a(120)+3*a(122)+3*a(123)+3*a(125))/3
a(49)=315-a(98)-a(100)-a(123)-a(125)
a(48)=(945+a(98)-4*a(99)+2*a(100)-3*a(117)-a(118)+a(119)-2*a(120)-3*a(122)-3*a(124))/3
a(47)=(-945-a(98)+4*a(99)+a(100)+3*a(117)+a(118)-a(119)+2*a(120)+3*a(122)+3*a(124)+3*a(125))/3
a(46)=(945+a(98)-a(99)-a(100)-3*a(117)-a(118)+a(119)-2*a(120)-3*a(122)-3*a(125))/3
a(45)=(945+a(95)-2*a(98)-a(99)-2*a(100)-a(117)-a(118)-2*a(120)-3*a(123)+a(124)-3*a(125))/2
a(44)=(1134-3*a(95)+2*a(98)-2*a(99)+a(100)-3*a(117)-2*a(118)-a(119)-4*a(120)-3*a(122)+3*a(123)-3*a(124))/3
a(43)=(378+a(98)+2*a(99)-a(100)+2*a(118)-2*a(119)+a(120)-3*a(122)-3*a(124))/3
a(42)=(-378+3*a(95)-a(98)-2*a(99)+a(100)-2*a(118)+2*a(119)+2*a(120)+3*a(122)+3*a(124))/3
a(41)=(-3213-3*a(95)+2*a(98)+7*a(99)+4*a(100)+9*a(117)+7*a(118)+2*a(119)+8*a(120)+6*a(122)+3*a(123)+3*a(124)+9*a(125))/6
a(40)=(945-9*a(95)+2*a(98)+a(99)+4*a(100)-3*a(117)+a(118)+2*a(119)-4*a(120)-6*a(122)+3*a(123)-3*a(124)+3*a(125))/6
a(39)=(1701+3*a(95)+2*a(98)+a(99)-2*a(100)-3*a(117)+a(118)-4*a(119)-4*a(120)-6*a(122)-3*a(123)-3*a(124)-3*a(125))/6
a(38)=-63-a(118)+a(122)+a(123)+a(124)
a(37)=(-189-a(95)+2*a(98)+a(99)+a(117)+3*a(118)+2*a(120)-2*a(122)+a(123)-3*a(124)+a(125))/2
a(36)=(189+9*a(95)-10*a(98)-5*a(99)-2*a(100)+3*a(117)-5*a(118)+2*a(119)+2*a(120)+12*a(122)-9*a(123)+9*a(124)-3*a(125))/6
a(35)=(-945+9*a(95)-2*a(98)-a(99)+2*a(100)+3*a(117)-a(118)-2*a(119)+4*a(120)+6*a(122)-3*a(123)+3*a(124)+3*a(125))/6
a(34)=(-1701-3*a(95)-2*a(98)+5*a(99)+2*a(100)+3*a(117)-a(118)+4*a(119)+4*a(120)+6*a(122)+3*a(123)+9*a(124)+3*a(125))/6
a(33)=63+a(98)+a(118)-a(122)-a(124)
a(32)=(567+3*a(95)-8*a(98)-a(99)-4*a(100)+3*a(117)-7*a(118)-2*a(119)-2*a(120)+12*a(122)-3*a(123)+9*a(124)-3*a(125))/6
a(31)=(1197-3*a(95)+2*a(98)-a(99)-3*a(117)+a(118)-2*a(120)-6*a(122)+a(123)-5*a(124)-a(125))/2
a(30)=(945-3*a(95)+2*a(98)+a(99)-2*a(100)-3*a(117)+a(118)+2*a(119)+2*a(120)-6*a(122)+3*a(123)-3*a(124)-3*a(125))/6
a(29)=(-1134+3*a(95)+a(98)-a(99)+2*a(100)+3*a(117)+2*a(118)+a(119)+4*a(120)+3*a(122)+3*a(125))/3
a(28)=(-378-5*a(98)+2*a(99)-a(100)+3*a(117)-a(118)+a(119)+a(120)+6*a(122)-3*a(123)+6*a(124))/3
a(27)=756-a(95)+a(98)-a(99)-2*a(117)-2*a(120)-3*a(122)-2*a(124)-a(125)
a(26)=(-189+a(95)+a(99)+a(117)-a(118)-2*a(119)+2*a(122)+a(123)+a(124)+a(125))/2
a(25)=315-a(100)-a(122)-a(123)-a(125)
a(24)=-a(99)+a(123)+a(125)
a(23)=-a(98)+a(122)+a(124)
a(22)=(945+a(98)-a(99)+2*a(100)-3*a(117)-a(118)+a(119)-2*a(120)-3*a(122)-3*a(124)-3*a(125))/3
a(21)=(-945+2*a(98)+4*a(99)+a(100)+3*a(117)+a(118)-a(119)+2*a(120)+3*a(122)+3*a(125))/3
a(20)=315-a(95)-a(117)-a(118)-a(120)
a(19)=(1323-a(95)-a(99)-2*a(100)-3*a(117)+a(118)-2*a(120)-4*a(122)-a(123)-3*a(124)-3*a(125))/2
a(18)=(189+2*a(98)-2*a(99)+a(100)+a(118)+2*a(119)-a(120)-3*a(122)+3*a(123)-3*a(124))/3
a(17)=(-3213+3*a(95)+2*a(98)+7*a(99)+4*a(100)+9*a(117)+7*a(118)-4*a(119)+8*a(120)+6*a(122)+3*a(123)+3*a(124)+9*a(125))/6
a(16)=-189+a(95)-a(98)+a(117)-a(118)+a(120)+2*a(122)-a(123)+2*a(124)
a(15)=(315+a(95)-2*a(98)-a(99)-a(117)-a(118)+2*a(122)-a(123)+a(124)-a(125))/2
a(14)=(1134-3*a(95)+2*a(98)+a(99)+a(100)-3*a(117)-2*a(118)+2*a(119)-4*a(120)-3*a(122)-3*a(124)-3*a(125))/3
a(13)=(378+4*a(98)+2*a(99)-a(100)+5*a(118)-2*a(119)+a(120)-6*a(122)-6*a(124))/3
a(12)=(-1323+3*a(95)-2*a(98)-a(99)-a(100)+6*a(117)-a(118)+a(119)+4*a(120)+6*a(122)+6*a(124)+3*a(125))/3
a(11)=(567-3*a(95)-2*a(98)-a(99)+2*a(100)-3*a(117)-a(118)-2*a(119)-2*a(120)+3*a(123)+3*a(124)+3*a(125))/6
a(10)=(945-3*a(95)+2*a(98)+a(99)+4*a(100)-3*a(117)+a(118)+2*a(119)-4*a(120)-6*a(122)+3*a(123)-3*a(124)-3*a(125))/6
a(9)=(-1134+3*a(95)+a(98)+2*a(99)+2*a(100)+3*a(117)+2*a(118)-2*a(119)+4*a(120)+3*a(122)+3*a(125))/3
a(8)=(-378-2*a(98)+2*a(99)-a(100)+3*a(117)-4*a(118)+a(119)+a(120)+6*a(122)-3*a(123)+6*a(124))/3
a(7)=(2268-3*a(95)+2*a(98)-2*a(99)-2*a(100)-6*a(117)+a(118)-a(119)-4*a(120)-9*a(122)-6*a(124)-3*a(125))/3
a(6)=(-567+3*a(95)-4*a(98)-5*a(99)-2*a(100)+3*a(117)+a(118)+2*a(119)+2*a(120)+6*a(122)+3*a(123)+3*a(124)+3*a(125))/6
a(5)=(-1890+3*a(95)+2*a(98)+a(99)+a(100)+6*a(117)+4*a(118)-a(119)+5*a(120)+3*a(122)+3*a(123)+6*a(125))/3
a(4)=(-693+a(95)-2*a(98)+a(99)+3*a(117)-a(118)+2*a(120)+4*a(122)-a(123)+5*a(124)+a(125))/2
a(3)=(756-a(98)-2*a(99)+a(100)-3*a(117)-2*a(118)-a(119)-a(120))/3
a(2)=(1323-3*a(95)-4*a(98)+a(99)-2*a(100)-3*a(117)-5*a(118)+2*a(119)-4*a(120)+6*a(122)-3*a(123)+3*a(124)-3*a(125))/6
a(1)=(2457-3*a(95)+4*a(98)-a(99)-a(100)-6*a(117)+2*a(118)+a(119)-5*a(120)-12*a(122)-9*a(124)-6*a(125))/3

The linear equations shown above, are ready to be solved, for the magic constant 315.

The solutions can be obtained by guessing a(122) ... a(125), a(117) ... a(120), a(98) ... a(100) and a(95) and filling out these guesses in the abovementioned equations.

For distinct integers also following relations should be applied:

0 < a(i) =< 125       for i = 1 ... 94, 96, 97, 101 ... 116, 121
Int(a(i)) = a(i)      for all broken equations
a(i) ≠ a(j)           for i ≠ j

which can be incorporated in a guessing routine, which might be used to find other 5^th order Pantriagonal Magic Cubes.

However, the equations deducted above can be applied in a more efficient method to generate Moriyama Pantriagonal Magic Cubes, which will be discussed in Section 5.6a.

4.9.3 Analytic Solution (2)

Although not consisered in the analysis above, the Moryama Cube is an Associated Pantriagonal Magic Cube.

This results in following additional equations:

a(1) + a(125) = 126
a(2) + a(124) = 126
a(3) + a(123) = 126
a(4) + a(122) = 126
a(5) + a(121) = 126
a(6) + a(120) = 126
a(7) + a(119) = 126
a(8) + a(118) = 126
a(9) + a(117) = 126
a(10) + a(116) = 126
a(11) + a(115) = 126
a(12) + a(114) = 126
a(13) + a(113) = 126
a(14) + a(112) = 126
a(15) + a(111) = 126
a(16) + a(110) = 126

a(17) + a(109) = 126
a(18) + a(108) = 126
a(19) + a(107) = 126
a(20) + a(106) = 126
a(21) + a(105) = 126
a(22) + a(104) = 126
a(23) + a(103) = 126
a(24) + a(102) = 126
a(25) + a(101) = 126
a(26) + a(100) = 126
a(27) + a(99) = 126
a(28) + a(98) = 126
a(29) + a(97) = 126
a(30) + a(96) = 126
a(31) + a(95) = 126
a(32) + a(94) = 126

a(33) + a(93) = 126
a(34) + a(92) = 126
a(35) + a(91) = 126
a(36) + a(90) = 126
a(37) + a(89) = 126
a(38) + a(88) = 126
a(39) + a(87) = 126
a(40) + a(86) = 126
a(41) + a(85) = 126
a(42) + a(84) = 126
a(43) + a(83) = 126
a(44) + a(82) = 126
a(45) + a(81) = 126
a(46) + a(80) = 126
a(47) + a(79) = 126
a(48) + a(78) = 126

a(49) + a(77) = 126
a(50) + a(76) = 126
a(51) + a(75) = 126
a(52) + a(74) = 126
a(53) + a(73) = 126
a(54) + a(72) = 126
a(55) + a(71) = 126
a(56) + a(70) = 126
a(57) + a(69) = 126
a(58) + a(68) = 126
a(59) + a(67) = 126
a(60) + a(66) = 126
a(61) + a(65) = 126
a(62) + a(64) = 126

which can be added to the equations deducted in Section 4.9.2 above and results finally in following linear equations:

a(121) = 315 - a(122) - a(123) - a(124) - a(125)
a(116) = 315 - a(117) - a(118) - a(119) - a(120)
a(115) = 315 - a(117) - a(118) - a(120) - a(125)
a(114) =       a(118) + a(120) - a(124)
a(113) =       a(117) + a(119) - a(123)
a(112) = 315 - a(117) - a(119) - a(120) - a(122)
a(111) = 315 - a(112) - a(113) - a(114) - a(115)
a(110) =       a(111) + a(118) - a(124)
a(109) = 315 - a(118) - a(120) - a(123) - a(125)
a(108) = 315 - a(117) - a(119) - a(122) - a(124)
a(107) = 315 - a(116) - a(118) - a(121) - a(123)
a(106) = 315 - a(107) - a(108) - a(109) - a(110)
a(105) = 315 - a(110) - a(115) - a(120) - a(125)
a(104) = 315 - a(109) - a(114) - a(119) - a(124)
a(103) = 315 - a(108) - a(113) - a(118) - a(123)
a(102) = 315 - a(107) - a(112) - a(117) - a(122)
a(101) = 315 - a(106) - a(111) - a(116) - a(121)
a(100) = 189 - a(116) - a(123)
a( 99) = 189 - a(117) - a(122) + a(123) - a(124)
a( 98) =-126 - a(118) + 2 * a(122) + 2 * a(124)
a( 97) = 189 - a(119) - a(122) + a(123) - a(124)
a( 96) = 315 - a( 97) - a( 98) - a( 99) - a(100)
a( 95) = 504 - 2 * a(117) - a(118) - 2 * a(120) - a(122) - a(125)
a( 94) = 189 - a(116) + a(120) - a(121) - a(123)
a( 93) = 189 - a(122) - a(124)
a( 92) = 189 + a(116) - a(120) - a(123) - a(125)
a( 91) = 315 - a( 92) - a( 93) - a( 94) - a( 95)
a( 90) =-126 + 2 * a(117) + a(118) + 3 * a(120) - 2 * a(121) - a(124)
a( 89) = 189 - a(117) - a(118) - 2 * a(120) + a(121) + a(124)
a( 88) =-126 + a(118) + a(121) + a(125)
a( 87) =  63 - a( 95) + a(119)
a( 86) = 315 - a( 87) - a( 88)- a( 89) - a( 90)
a( 85) = 819 - 2 * a(117) - 2 * a(118) - a(119) - 3 * a(120) - a(122) - a(123) - 2 * a(125)
a( 84) = 189 - a(116) - 2 * a(119) + a(123) - a(124) + a(125)
a( 83) =  63 - a( 97) + a(117)
a( 82) = 504 - 2 * a(117) - a(120) - 2 * a(122) - a(124) - a(125)
a( 81) = 315 - a( 82) - a( 83) - a( 84) - a( 85)
a( 80) = 315 - a( 85) - a( 90) - a( 95) - a(100)
a( 79) = 315 - a( 84) - a( 89) - a( 94) - a( 99)
a( 78) = 315 - a( 83) - a( 88) - a( 93) - a( 98)
a( 77) = 315 - a( 82) - a( 87) - a( 92) - a( 97)
a( 76) = 315 - a( 81) - a( 86) - a( 91) - a( 96)
a( 75) = 378 - a(117) - a(120) - a(122) - a(124) - a(125)
a( 74) =-252 + a(117) + a(119) + a(120) + 2 * a(122) - a(123) + a(124)
a( 73) = 378 - a(117) - a(119) - 2 * a(122) + a(123) - 2 * a(124)
a( 72) =-126 + a( 79) + a(124) + a(125)
a( 71) = 315 - a( 72) - a( 73) - a( 74) - a(75)
a( 70) = 252 - a( 86) - a(121) - a(125)
a( 69) = 252 - a( 87) - a(122) - a(124)
a( 68) =  63 - a(118) + a(122) - a(123) + a(124)
a( 67) = 189 + a( 91) - a(117) - a(122) - a(124)
a( 66) = 315 - a( 67) - a( 68) - a( 69) - a( 70)
a( 65) = 189 + a( 86) - a(120) - a(122) - a(123)
a( 64) = 189 + a( 81) - a(119) - a(120) - a(122)

a(63) = 63
a(62) = 126 - a(64)
a(61) = 126 - a(65)
a(60) = 126 - a(66)
a(59) = 126 - a(67)
a(58) = 126 - a(68)
a(57) = 126 - a(69)
a(56) = 126 - a(70)
a(55) = 126 - a(71)
a(54) = 126 - a(72)
a(53) = 126 - a(73)
a(52) = 126 - a(74)
a(51) = 126 - a(75)
a(50) = 126 - a(76)
a(49) = 126 - a(77)

a(48) = 126 - a(78)
a(47) = 126 - a(79)
a(46) = 126 - a(80)
a(45) = 126 - a(81)
a(44) = 126 - a(82)
a(43) = 126 - a(83)
a(42) = 126 - a(84)
a(41) = 126 - a(85)
a(40) = 126 - a(86)
a(39) = 126 - a(87)
a(38) = 126 - a(88)
a(37) = 126 - a(89)
a(36) = 126 - a(90)
a(35) = 126 - a(91)
a(34) = 126 - a(92)
a(33) = 126 - a(93)

a(32) = 126 - a(94)
a(31) = 126 - a(95)
a(30) = 126 - a(96)
a(29) = 126 - a(97)
a(28) = 126 - a(98)
a(27) = 126 - a(99)
a(26) = 126 - a(100)
a(25) = 126 - a(101)
a(24) = 126 - a(102)
a(23) = 126 - a(103)
a(22) = 126 - a(104)
a(21) = 126 - a(105)
a(20) = 126 - a(106)
a(19) = 126 - a(107)
a(18) = 126 - a(108)
a(17) = 126 - a(109)

a(16) = 126 - a(110)
a(15) = 126 - a(111)
a(14) = 126 - a(112)
a(13) = 126 - a(113)
a(12) = 126 - a(114)
a(11) = 126 - a(115)
a(10) = 126 - a(116)
a(9) = 126 - a(117)
a(8) = 126 - a(118)
a(7) = 126 - a(119)
a(6) = 126 - a(120)
a(5) = 126 - a(121)
a(4) = 126 - a(122)
a(3) = 126 - a(123)
a(2) = 126 - a(124)
a(1) = 126 - a(125)

Also these equations can be applied in an efficient method to generate Associated Pantriagonal Magic Cubes, which will be discussed in Section 5.6b.

Index

About the Author