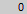Office Applications and Entertaiment, Magic Squares

Pan Magic Squares 7 x 7, Interactive Solution, Sudoku Method

Introduction

Pan Magic Squares of the 7^th order can be constructed by means of following Sudoku Comparable Method:

1. Fill the first row of square A and square B with the numbers 0, 1, 2, 3, 4, 5 and 6.
   While starting with 0 there are 6! = 720 possible combinations for each square.
   
   
2. Complete square A and B by copying the first row into the following rows of the applicable square, according to one of the following schemes:
   
   
   1. A: shift 2 columns to the left / B: shift 2 columns to the right
   2. A: shift 2 columns to the left / B: shift 3 columns to the right
   3. A: shift 2 columns to the left / B: shift 3 columns to the left
   4. A: shift 3 columns to the left / B: shift 2 columns to the right
   5. A: shift 3 columns to the left / B: shift 3 columns to the right
   6. A: shift 3 columns to the left / B: shift 2 columns to the left
      
      
3. Construct the final square C by means of the matrix operation C = 7 * A + B + [1].

	Squares A B C C = 7 * A + B + [1] First Row A 1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6 7 8 First Row B 1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6 Completion Scheme: 1 2 3 4 5 6

Procedure:

1. Select one of the matrix completion schemes, as described in point 2 of the introduction above (default = 1).
   
   
2. Select the first row of matrix A with the left  selection buttons, and confirm by pushing button 'Matrix A'.
   
   
3. Select the first row of matrix B with the right selection buttons, and confirm by pushing button 'Matrix B'.
   
   
4. Press the button ‘Square’ to calculate and visualise the resulting Pan Magic Square.
   
   
5. Select a Base Square with the selection button left from the button 'SubCls'. Select:
   
   
   1. for square C   (default);
   2. for Horizontal Reflection of square C;
   3. for Vertical   Reflection of square C;
   4. for  90 degr   Rotation   of square C;
   5. for Horizontal Reflection of 90 degr Rotated Square C;
   6. for Vertical   Reflection of 90 degr Rotated Square C;
   7. for 180 degr   Rotation of C;
   8. for 270 degr   Rotation of C.
      
      
6. Press the button ‘SubCls’ to visualise the related Sub Class (49 elements) based on row/column shifts of the selected Base Square.
   
   

The possible combinations of square A and B described above will result in 6 * 720 * 720 /4 = 777.600 unique solutions.

Each of these 777.600 Pan Magic Squares will result in a unique Class C_n and finally in 777.600 * 49 * 8 = 304.819.200 possible Pan Magic Squares of the 7^th order.

Have Fun!