Office Applications and Entertainment, Magic Squares

6.12   Pan Magic Squares, Non Consecutive Integers, Part 2
       Misc. Symmetries

6.12.1 Introduction

In Section 6.09 following symmetries:

• Associated: All pairs of elements, which can be connected with a straight line through the center, sum to 2 * s1 / n
• Complete  : All pairs of elements distant n / 2 along a main - or pan diagonal sum to 2 * s1 / n

have been applied - in combination with other properties - on Pan Magic Squares based on non consecutive integers.

Miscellaneous additional symmetries have been introduced in Section 6.11 and applied on Simple Magic Squares (consecutive integers).

In following sections these newly introduced symmetries will be - as far as possible - applied on Pan Magic Squares, consequently based on non consecutive integers.

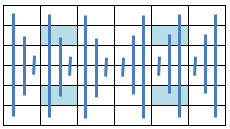
6.12.2 Axial Symmetric Pan Magic Squares

When the equations defining the Axial Symmetry as illustrated below:

are added to the equations describing a Pan Magic Square of the sixth order (ref. Section 6.1), the resulting Axial Symmetric Pan Magic Square can be described by following set of linear equations:

a(31) =   s1   - a(32) - a(33) - a(34) - a(35) - a(36)
a(25) =   s1   - a(26) - a(27) - a(28) - a(29) - a(30)
a(24) = - s1/2 + a(26) + a(27) + a(28) + a(33)
a(23) =   s1/2 - a(28) - a(29) - a(30) + a(32)
a(22) = 3*s1/2 - a(27) - a(28) - a(29) - a(32) - a(33) - a(34) - a(35) - a(36)
a(21) =   s1/2 - a(26) - a(27) - a(28) + a(36)
a(20) = - s1/2 + a(28) + a(29) + a(30) + a(35)
a(19) = - s1/2 + a(27) + a(28) + a(29) + a(34)

The solutions can be obtained by guessing:

      a(26) ... a(30) and a(32) ... a(36)

and filling out these guesses in the abovementioned equations.

The minimum Magic Sum s1 = 120 occurs for the range {i} = {1 ... 13, 15 ... 19, 21 ... 25, 27 ... 39}.

Attachment 6.12.2 shows the first occuring Axial Symmetric Pan Magic Squares for a(36) = i (ref. MgcSqr6122).

6.12.3 Row Symmetric Pan Magic Squares (Type 1)

When the equations defining the Row Symmetry as illustrated below:

are added to the equations describing a Pan Magic Square of the sixth order (ref. Section 6.1), the resulting Row Symmetric Pan Magic Square can be described by following set of linear equations:

a(31) =  s1   - a(32) - a(33) - a(34) - a(35) - a(36)
a(23) =       - a(24) + a(35) + a(36)
a(22) =         a(24) + a(34) - a(36)
a(21) =       - a(24) + a(33) + a(36)
a(20) =         a(24) + a(32) - a(36)
a(19) =  s1   - a(24) - a(32) - a(33) - a(34) - a(35)
a(12) =  s1/2 - a(24) - a(32) - a(34) + a(36)
a(11) = -s1/2 + a(24) + a(32) + a(34) + a(35)
a(10) =  s1/2 - a(24) - a(32)
a(9) =  -s1/2 + a(24) + a(32) + a(33) + a(34)
a(8) =   s1/2 - a(24) - a(34)
a(7) =   s1/2 + a(24) - a(33) - a(35) - a(36)

The solutions can be obtained by guessing

      a(24) and a(32) ... a(36)

and filling out these guesses in the abovementioned equations.

The minimum Magic Sum s1 = 126 occurs within the range {i} = {1, 3 ... 7, 9 ... 20, 22 ...33, 35 ... 39, 41}.

An optimized guessing routine (MgcSqr6123), produced 1728 Row Symmetric Pan Magic Squares within 1,2 hours, of which the first occuring for a(36) = i are shown in Attachment 6.12.3.

6.12.4 Row Symmetric Pan Magic Squares (Type 2)

When the equations defining the Row Symmetry as illustrated below:

are added to the equations describing a Pan Magic Square of the sixth order (ref. Section 6.1), the resulting Row Symmetric Pan Magic Square can be described by following set of linear equations:

a(31) =    s1  - a(32) - a(33) - a(34) - a(35) - a(36)
a(27) =  2*s1 - 2 * a(28) - 2 * a(29) - a(30) - a(33) - 2 * a(34) - 2 * a(35) - a(36)
a(26) = -2*s1 + 2 * a(28) + 3 * a(29) + 2 * a(30) - a(32) + 2 * a(34) + 3 * a(35) + 2 * a(36)
a(25) =    s1 - a(28) - 2 * a(29) - 2 * a(30) + a(32) + a(33) - a(35) - a(36)
a(22) =  - s1/2 - a(23) - a(24) + a(28) + a(29) + a(30) - a(32) + a(34) + 2 * a(35) + a(36)
a(21) =    s1   + a(24) - 2 * a(28) - 2 * a(29) - 2 * a(30) + 2 * a(32) + a(33) - 2 * a(35) - a(36)
a(20) =  - s1   + a(23) + 2 * a(28) + 2 * a(29) + 2 * a(30) - a(32) + a(35)
a(19) =  3*s1/2 - a(23) - a(24) - a(28) - a(29) - a(30) - a(33) - a(34) - a(35)

The solutions can be obtained by guessing

      (23), a(24), a(28) ... a(30) and a(32) ... a(36)

and filling out these guesses in the abovementioned equations.

The minimum Magic Sum s1 = 120 occurs for the range {i} = {1 ... 13, 15 ... 19, 21 ... 25, 27 ... 39}.

Attachment 6.12.4 shows the first occuring Row Symmetric Pan Magic Squares for a(36) = i (ref. MgcSqr6124).

6.12.5 Crosswise Symmetric Pan Magic Squares

When the equations defining the Crosswise Symmetry as illustrated below:

are added to the equations describing a Pan Magic Square of the sixth order (ref. Section 6.1), the resulting Crosswise Symmetric Pan Magic Square can be described by following set of linear equations:

a(31) =  s1   - a(32) - a(33) - a(34) - a(35) - a(36)
a(22) =       - a(23) + a(33) + a(36)
a(20) =  s1   - a(21) - a(32) - a(33) - a(35) - a(36)
a(19) =       - a(24) + a(32) + a(35)
a(12) =  s1/2 + a(23) - a(32) - a(33) - a(36)
a(11) =  s1/2 + a(24) - a(32) - a(33) - a(35)
a(10) = -s1/2 + a(21) + a(32) + a(33) + a(35)
a( 9) = -s1/2 - a(23) + a(32) + a(33) + a(34) + a(35) + a(36)
a( 8) =  s1/2 - a(24) - a(34)
a( 7) =  s1/2 - a(21) - a(35)

The solutions can be obtained by guessing:

      (21), a(23), a(24) and a(32) ... a(36)

and filling out these guesses in the abovementioned equations.

The minimum Magic Sum s1 = 120 occurs for the range {i} = {1 ... 13, 15 ... 19, 21 ... 25, 27 ... 39}.

Attachment 6.12.5 shows the first occuring Crosswise Symmetric Pan Magic Squares for a(36) = i (ref. MgcSqr6125).

6.12.7 Symmetric Pan Magic Squares (Type 4)

When the equations defining the assorted symmetry as illustrated below:

are added to the equations describing a Pan Magic Square of the sixth order (ref. Section 6.1), the resulting Symmetric Pan Magic Square can be described by following set of linear equations:

a(31) =   s1   - a(32) - a(33) - a(34) - a(35) - a(36)
a(27) = 3*s1/2 - a(28) - a(29) - a(32) - a(33) - 2 * a(34) - a(35) - a(36)
a(26) =  -s1   + a(29) + a(32) + 2 * a(34) + a(35) + 2 * a(36)
a(25) =   s1/2 - a(29) - a(30) + a(33) - a(36)
a(23) =   s1/2 - a(28) - a(29) - a(30) + a(32)
a(22) =        - a(24) + a(34) + a(36)
a(21) =          a(24) + a(33) - a(36)
a(20) =  -s1/2 + a(28) + a(29) + a(30) + a(35)
a(19) =   s1   - a(24) - a(32) - a(33) - a(34) - a(35)

The solutions can be obtained by guessing:

      (24), a(28) ... a(30) and a(32) ... a(36)

and filling out these guesses in the abovementioned equations.

The minimum Magic Sum s1 = 120 occurs for the range {i} = {1 ... 13, 15 ... 19, 21 ... 25, 27 ... 39}.

Attachment 6.12.7 shows the first occuring Symmetric Pan Magic Squares for a(36) = i (ref. MgcSqr6127)

6.12.8 Summary

The obtained results regarding the miscellaneous types of order 6 Pan Magic Squares as deducted and discussed in previous sections are summarized in following table:

Comparable routines as listed above, can be used to generate order 7 (Pan) Magic Squares, which will be described in following sections.