Office Applications and Entertainment, Magic Squares

14.0    Special Magic Squares, Prime Numbers

14.4.20 Symmetric Magic Squares (6 x 6)

In previous sections following possible symmetries have been introduced:

• Associated: All pairs of elements, which can be connected with a straight line through the center, sum to 2 * s1 / n
• Complete  : All pairs of elements distant n / 2 along a main - or pan diagonal sum to 2 * s1 / n

and applied in combination with other properties.

In following sections miscellaneous additional symmetries will be introduced and - as far as possible - applied on Prime Number (Pan) Magic Squares.

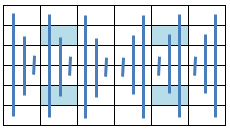
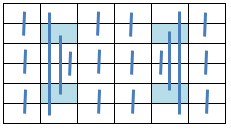
14.4.21 Axial Symmetric Pan Magic Squares

When the equations defining the Axial Symmetry as illustrated below:

are added to the equations describing a Pan Magic Square of the sixth order, the resulting Axial Symmetric Pan Magic Square can be described by following set of linear equations:

a(31) =   s1   - a(32) - a(33) - a(34) - a(35) - a(36)
a(25) =   s1   - a(26) - a(27) - a(28) - a(29) - a(30)
a(24) = - s1/2 + a(26) + a(27) + a(28) + a(33)
a(23) =   s1/2 - a(28) - a(29) - a(30) + a(32)
a(22) = 3*s1/2 - a(27) - a(28) - a(29) - a(32) - a(33) - a(34) - a(35) - a(36)
a(21) =   s1/2 - a(26) - a(27) - a(28) + a(36)
a(20) = - s1/2 + a(28) + a(29) + a(30) + a(35)
a(19) = - s1/2 + a(27) + a(28) + a(29) + a(34)

which can be incorporated in a routine to generate subject Axial Symmetric Pan Magic Squares (ref. MgcSqr6122).

Attachment 6.12.2 shows for miscellaneous Magic Sums (24 ea) the first occurring Prime Number Axial Symmetric Pan Magic Square.

Each square shown corresponds with numerous squares for the applicable Magic Sum and variable values {a_i}.

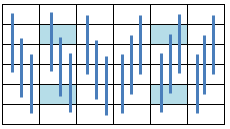
14.4.22 Row Symmetric Pan Magic Squares (Type 1)

When the equations defining the Row Symmetry as illustrated below:

are added to the equations describing a Pan Magic Square of the sixth order, the resulting Row Symmetric Pan Magic Square can be described by following set of linear equations:

a(31) =  s1   - a(32) - a(33) - a(34) - a(35) - a(36)
a(23) =       - a(24) + a(35) + a(36)
a(22) =         a(24) + a(34) - a(36)
a(21) =       - a(24) + a(33) + a(36)
a(20) =         a(24) + a(32) - a(36)
a(19) =  s1   - a(24) - a(32) - a(33) - a(34) - a(35)
a(12) =  s1/2 - a(24) - a(32) - a(34) + a(36)
a(11) = -s1/2 + a(24) + a(32) + a(34) + a(35)
a(10) =  s1/2 - a(24) - a(32)
a(9) =  -s1/2 + a(24) + a(32) + a(33) + a(34)
a(8) =   s1/2 - a(24) - a(34)
a(7) =   s1/2 + a(24) - a(33) - a(35) - a(36)

which can be incorporated in a routine to generate subject Row Symmetric Pan Magic Squares (MgcSqr6123).

Attachment 6.12.3 shows for miscellaneous Magic Sums (15 ea) the first occurring Prime Number Row Symmetric Pan Magic Square.

Each square shown corresponds with numerous squares for the applicable Magic Sum and variable values {a_i}.

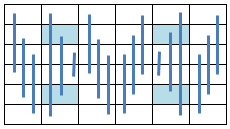
14.4.23 Row Symmetric Pan Magic Squares (Type 2)

When the equations defining the Row Symmetry as illustrated below:

are added to the equations describing a Pan Magic Square of the sixth order, the resulting Row Symmetric Pan Magic Square can be described by following set of linear equations:

a(31) =    s1  - a(32) - a(33) - a(34) - a(35) - a(36)
a(27) =  2*s1 - 2 * a(28) - 2 * a(29) - a(30) - a(33) - 2 * a(34) - 2 * a(35) - a(36)
a(26) = -2*s1 + 2 * a(28) + 3 * a(29) + 2 * a(30) - a(32) + 2 * a(34) + 3 * a(35) + 2 * a(36)
a(25) =    s1 - a(28) - 2 * a(29) - 2 * a(30) + a(32) + a(33) - a(35) - a(36)
a(22) =  - s1/2 - a(23) - a(24) + a(28) + a(29) + a(30) - a(32) + a(34) + 2 * a(35) + a(36)
a(21) =    s1   + a(24) - 2 * a(28) - 2 * a(29) - 2 * a(30) + 2 * a(32) + a(33) - 2 * a(35) - a(36)
a(20) =  - s1   + a(23) + 2 * a(28) + 2 * a(29) + 2 * a(30) - a(32) + a(35)
a(19) =  3*s1/2 - a(23) - a(24) - a(28) - a(29) - a(30) - a(33) - a(34) - a(35)

which can be incorporated in a routine to generate subject Row Symmetric Pan Magic Squares (MgcSqr6124).

Attachment 6.12.4 shows for miscellaneous Magic Sums (24 ea) the first occurring Prime Number Row Symmetric Pan Magic Square.

Each square shown corresponds with numerous squares for the applicable Magic Sum and variable values {a_i}.

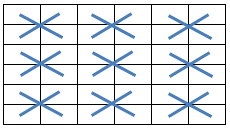
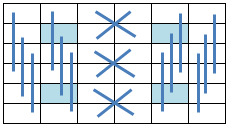
14.4.24 Crosswise Symmetric Pan Magic Squares

When the equations defining the Crosswise Symmetry as illustrated below:

are added to the equations describing a Pan Magic Square of the sixth order, the resulting Crosswise Symmetric Pan Magic Square can be described by following set of linear equations:

a(31) =  s1   - a(32) - a(33) - a(34) - a(35) - a(36)
a(22) =       - a(23) + a(33) + a(36)
a(20) =  s1   - a(21) - a(32) - a(33) - a(35) - a(36)
a(19) =       - a(24) + a(32) + a(35)
a(12) =  s1/2 + a(23) - a(32) - a(33) - a(36)
a(11) =  s1/2 + a(24) - a(32) - a(33) - a(35)
a(10) = -s1/2 + a(21) + a(32) + a(33) + a(35)
a( 9) = -s1/2 - a(23) + a(32) + a(33) + a(34) + a(35) + a(36)
a( 8) =  s1/2 - a(24) - a(34)
a( 7) =  s1/2 - a(21) - a(35)

which can be incorporated in a routine to generate subject Crosswise Symmetric Pan Magic Squares (MgcSqr6125).

Attachment 6.12.5 shows for miscellaneous Magic Sums (24 ea) the first occurring Prime Number Crosswise Symmetric Pan Magic Square.

Each square shown corresponds with numerous squares for the applicable Magic Sum and variable values {a_i}.

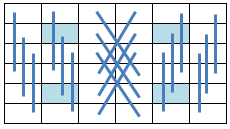
14.4.25 Symmetric Pan Magic Squares (Type 4)

When the equations defining the assorted symmetry as illustrated below:

are added to the equations describing a Pan Magic Square of the sixth order, the resulting Symmetric Pan Magic Square can be described by following set of linear equations:

a(31) =   s1   - a(32) - a(33) - a(34) - a(35) - a(36)
a(27) = 3*s1/2 - a(28) - a(29) - a(32) - a(33) - 2 * a(34) - a(35) - a(36)
a(26) =  -s1   + a(29) + a(32) + 2 * a(34) + a(35) + 2 * a(36)
a(25) =   s1/2 - a(29) - a(30) + a(33) - a(36)
a(23) =   s1/2 - a(28) - a(29) - a(30) + a(32)
a(22) =        - a(24) + a(34) + a(36)
a(21) =          a(24) + a(33) - a(36)
a(20) =  -s1/2 + a(28) + a(29) + a(30) + a(35)
a(19) =   s1   - a(24) - a(32) - a(33) - a(34) - a(35)

which can be incorporated in a routine to generate subject Symmetric Pan Magic Squares (MgcSqr6127).

Attachment 6.12.7 shows for miscellaneous Magic Sums (24 ea) the first occurring Prime Number Symmetric Pan Magic Square.

Each square shown corresponds with numerous squares for the applicable Magic Sum and variable values {a_i}.

14.4.26 Symmetric Magic Squares (Type 3)

When the equations defining the assorted symmetry as illustrated below:

are added to the equations describing a Magic Square of the sixth order, the resulting Symmetric Magic Square can be described by following set of linear equations:

a(31) =     s1   - a(32) - a(33) - a(34) - a(35) - a(36)
a(26) = 2 * s1/3 - a(29) - a(32) - a(35)
a(19) =     s1   - a(20) - a(21) - a(22) - a(23) - a(24)
a(12) = 2 * s1/3 + a(21) - a(22) - 2 * a(29) + a(31) - a(32) - a(35)
a(9) =      s1   - a(10) - a(31) - a(32) - a(35) - a(36)
a(7) = -2 * s1/3 - a(21) + a(22) + 2 * a(29) + a(32) + a(35) + a(36)

which can be incorporated in a routine to generate subject Symmetric Magic Squares (MgcSqr6116).

Attachment 6.11.6 shows for miscellaneous Magic Sums (24 ea) the first occurring Prime Number Symmetric Magic Square.

Each square shown corresponds with numerous squares for the applicable Magic Sum and variable values {a_i}.

14.4.27 Symmetric Magic Squares (Type 5)

When the equations defining the assorted symmetry as illustrated below:

are added to the equations describing a Magic Square of the sixth order, the resulting Symmetric Magic Square can be described by following set of linear equations:

a(31) =    s1   - a(32) - a(33) - a(34) - a(35) - a(36)
a(25) =  4*s1/3 - a(26) - a(29) - a(30) - a(31) - a(32) - a(35) - a(36)
a(24) =           a(26) - a(29) + a(31)
a(21) =    s1   - a(22) - a(31) - a(32) - a(35) - a(36)
a(20) =         - a(23) + a(32) + a(35)
a(19) =         - a(26) + a(29) + a(36)
a(10) = (2*s1 - 2 * a(22) - 2 * a(31) - 2 * a(32) + a(33) - a(34) - 2*a(35) - 2*a(36))/2
a( 9) =    s1   - a(10) - a(31) - a(32) - a(35) - a(36)

which can be incorporated in a routine to generate subject Symmetric Magic Squares (MgcSqr6118).

Attachment 6.11.8 shows for miscellaneous Magic Sums (24 ea) the first occurring Prime Number Symmetric Magic Square.

Each square shown corresponds with numerous squares for the applicable Magic Sum and variable values {a_i}.

14.4.28 Symmetric Magic Squares (Type 6)

When the equations defining the assorted symmetry as illustrated below:

are added to the equations describing a Magic Square of the sixth order, the resulting Symmetric Magic Square can be described by following set of linear equations:

a(31) =  s1 - a(32) - a(33) - a(34) - a(35) - a(36)
a(25) =  s1 - a(26) - a(27) - a(28) - a(29) - a(30)
a(22) = -s1 + a(24) - a(26) + a(27) - a(28) + a(29) + a(32) + 3 * a(33) + a(35) + a(36)
a(21) = -s1 + a(24) - a(26) + a(29) + a(32) + 2 * a(33) + a(34) + a(35) + a(36)
a(20) = - 4 * a(21) - a(23) - 2 * a(27) + 2 * a(28) + a(32) + 4 * a(34) + a(35)
a(19) = -s1 + a(24) - 2 * a(26) + a(27) - a(28) + 2 * a(29) + a(32) + 3 * a(33) - a(34) + a(35) + 2*a(36)

which can be incorporated in a routine to generate subject Symmetric Magic Squares (MgcSqr6119).

Attachment 6.11.9 shows for miscellaneous Magic Sums (24 ea) the first occurring Prime Number Symmetric Magic Square.

Each square shown corresponds with numerous squares for the applicable Magic Sum and variable values {a_i}.

14.4.29 Summary

The obtained results regarding the miscellaneous types of order 6 Prime Number Symmetric Magic Squares as deducted and discussed in previous sections are summarized in following table:

Comparable routines as listed above, can be used to generate Prime Number Rectangular Compact Magic Squares of order 6, which will be described in Section 14.4.30.