|
Most Perfect Magic Squares 8 x 8, Interactive Solution based on Binary Matrices
Introduction
Comparable with the construction method for Pan Magic Squares (ref. Form4), Most Perfect Magic Squares can be constructed based on the binary representation of numbers
(0 = 000000, 1 = 000001, 2 = 000010, 3 = 000011 ... 63 = 111111).
Any Magic Square of order 8 with the numbers 1 ... 64 can be written as
B1 +
2 * B2 +
4 * B3 +
8 * B4 +
16 * B5 +
32 * B6 + [1],
where the matrices B1,
B2,
B3,
B4,
B5 and
B6
- further referred to as Binaries - contain only the numbers 0 and 1.
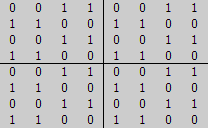
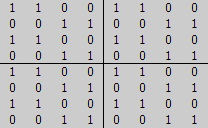
The 2 * 16 for Most Perfect Magic Squares applicable Binaries are shown in the windows 'Collection A' and 'Collection B' of the form below.
In order to achieve that the squares contain the distinct integers 1 ... 64, only 64 combinations of 3 horizontal and 3 vertical Binaries
(prefix H or V) are allowed, which can be selected in the form below.
Each of the Binaries can be selected from either Collection A or Collection B, resulting in 64 * 26 = 4096 possible combinations.
A Most Perfect Magic Square of order 8 can be constructed by means of the Matrix Operation MP =
B1 +
2 * B2 +
4 * B3 +
8 * B4 +
16 * B5 +
32 * B6 + [1].
 |
 |
|
Collection A
|
Collection B
|
Most Perfect Magic Square
|
|
|
|
|
|
|
|
Combination:
|
Collection/Sequence:
|
Automatic:
|
|
 |
 |
Procedure (Hand):
-
Select a combination of Binaries with the selection button left in the selection window.
-
Select for each of the Binaries collection A or B with the applicable selection buttons (select a or b).
-
Define the sequence with the applicable selection buttons (select 1, 2 ... 6 for
B1,
B2 ...
B6)
-
Press the button ‘Show Square’ to validate the selection and to calculate and visualise the resulting Most Perfect Magic Square.
The 4096 possible combinations and 6! = 720 permutations of the Binaries will result in 4096 * 720 = 2949120 different Most Perfect Magic Squares,
which number was found in Section 8.5.3 as well.
For Most Perfect Magic Squares with the Barink Restriction (property X) only selection 19 (default) will do, which results in 64 * 720 = 46080 different squares, which number was also found in Section 8.5.4.
Procedure (Automatic):
-
Built a Most Perfect Magic Square with property X as described above, and validate the square by pressing the button ‘Show Square’.
-
If you press the button ‘Report’, with all 6 Check Boxes checked (default), the report will contain only the Most Perfect Magic Square shown in the form.
-
By un checking more and more Check Boxes before pressing the button ‘Report’, more and more Most Perfect Magic Squares will be generated. Be careful with un checking to many Check Boxes, it might cause a time out error on your computer.
The algorithm used to generate the Magic Squares automatically is described in Section 8.5.4 and is based on the principle of Conditional Sequential Searching.
At start all independent variables have the value resulting from the constructed Most Perfect Magic Square in the form.
By un checking a Check Box, the related independant variable will vary between 1 and 64.
With only the Check Box for variable a(64) checked, 720 Most Perfect Magic Squares will be generated, which are shown in Attachment 8.5.4 for the value a(64) = 24.
Have Fun!
|







