Office Applications and Entertainment, Magic Squares

13.0 Construction of Single Magic Squares

13.1 Introduction

In previous sections several procedures were developed for sequential generation of Classes of (Pan) Magic Squares, based on couples of linear equations describing subject Classes.

Due to the vast amount of independent variables of the applied equations, the solutions could only be obtained by keeping a number of these variables constant.

Different clusters of solutions could be obtained by keeping other sets of independent variables constant.

In Section 22 was shown how single Magic Squares (order 4n) could be constructed based on (Pan) Magic Squares of
order 4.

Following sections provide some additional examples of the construction of single (Pan) Magic Squares of a certain order.

13.2 Pan Magic Squares, Odd

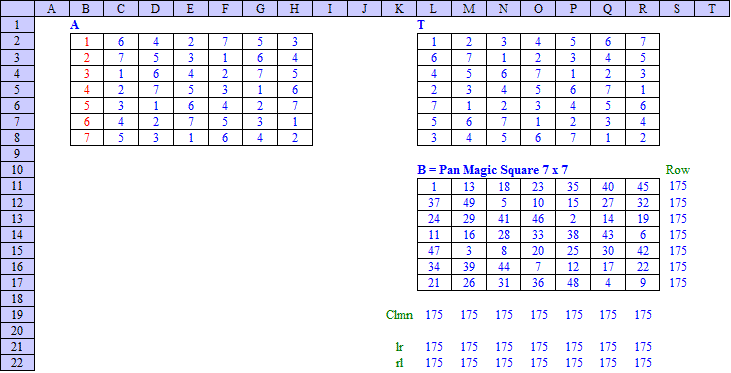
Pan Magic Squares (6n ± 1) × (6n ± 1)

Pan Magic Square of order 5, 7, 11, 13 ... (6n ± 1) can be constructed by means of following method:

1. Fill the first column of square A with the first (6n ± 1) natural numbers;
2. Copy the first column into the second column but shift it ring-wise by 2 rows;
3. Continue copying the current column into the next column with ring-wise shift by 2 rows until square A is filled completely;
4. Construct the transposed square T (exchange rows and columns);
5. Construct the final square B by means of the matrix operation B = (6n ± 1) * T + A - (6n ± 1).

As an example, subject method has been applied in an Excel spreadsheet for n = + 1, resulting in a Pan Magic Square of order 7, as shown below:

Pan Magic Squares, (6n + 3) × (6n + 3)

Pan Magic Squares of order 9, 15, 21 ... (6n + 3) can be constructed by means of following method:

1. Create a (2n + 1) × 3 rectangle with the first 6n + 3 natural numbers so that each column has the same sum.
   This can be done by starting with a 3 × 3 Magic Square and setup the rest cells of the rectangle in meander-style.
2. Copy this rectangle three times into square A so that the first 3 columns of the square are filled completely;
3. Copy the left 3 columns into the next 3 columns, but shift it ring-wise by 1 row.
4. Continue copying the current 3 columns into the next 3 columns, shifted ring-wise by 1 row, until square A is filled completely
5. Construct the transposed square T (exchange rows and columns).
6. Construct the final square B by means of the matrix operation B = (6n + 3) * T + A - (6n + 3).

As an example, subject method has been applied in an Excel spreadsheet for n = 1, resulting in a Pan Magic Square of order 9, as shown below:

13.3 Magic Squares, Odd

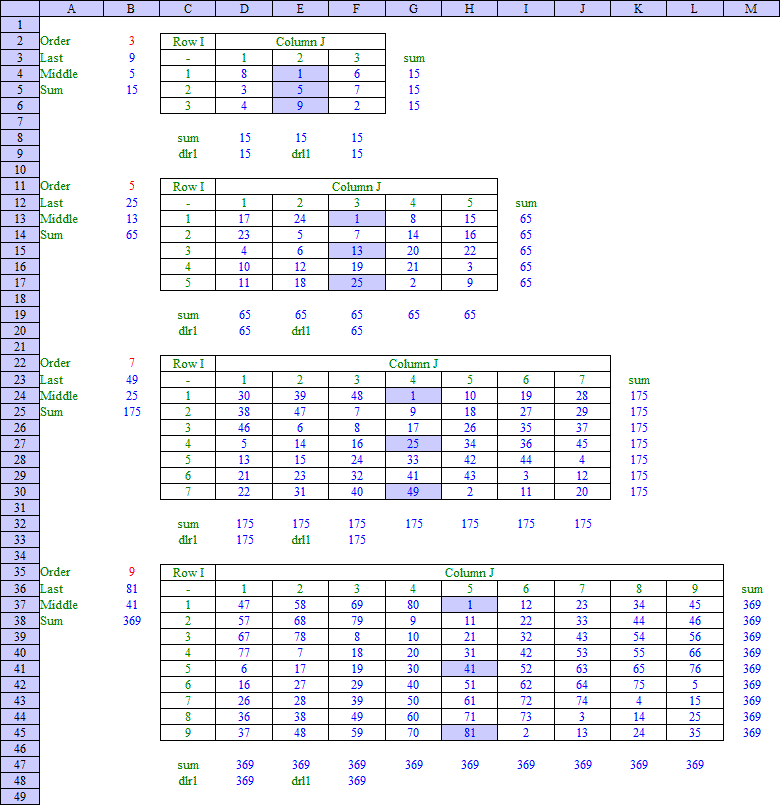
Magic Squares of odd order can be constructed based on the following formula's:

As an example, subject formula's have been applied for Magic Squares of order 3, 5, 7 and 9 in an Excel spreadsheet as shown below:

13.4 Pan Magic Squares, Even

Pan Magic Squares of order 6, 10, 14 ... (4n + 2) do not exist. For the 6^th order this has been proven in section 6.1.

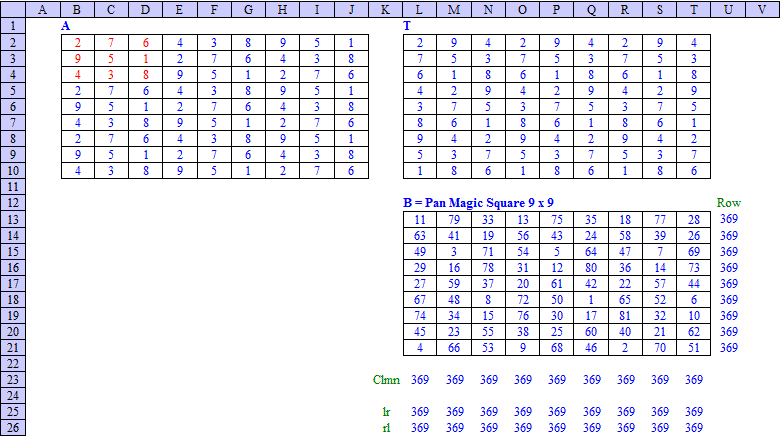
Pan Magic Squares, 4n × 4n

Pan Magic Squares of order 4, 8, 12 ... 4n can be constructed by means of following method:

1. Fill the first 2n columns of the first row of square A with 2n different natural numbers 1 =< n_i =< 4n;
2. Fill the first 2n columns of the second row with 2n other different natural numbers 1 =< n_i =< 4n, such that each vertical pair will have the same sum;
3. Copy the resulting 2 × 2n rectangle (2n - 1) times under the first rectangle;
4. Copy the resulting left 4n × 2n rectangle into the right 4n × 2n rectangle but shift it ring-wise by one row;
5. Construct a second square R by means of 90^o rotation of square A;
6. Construct square B by means of the matrix operation B = 4n * R + A - 4n.

As an example, subject method has been applied in an Excel spreadsheet for n = 2, resulting in a Pan Magic Square of order 8, as shown below:

Like the Franklin Squares, every 2 × 2 square in the resulting 4n × 4n Pan Magic Square will have the same sum.

Consequently the previous deducted pattern properties (ref. Section 8.4.3 and Attachment 8.4.3) will apply.

The resulting 4n × 4n square is also a Most Perfect Magic Square as defined in Section 2.4.

13.5 Interactive Solutions

Some of the construction methods described above, or comparable methods, have been applied in following Interactive Solutions:

• Form 4, Pan Magic Squares    4 x  4, Magic Constant   34, Binary Method
  
  
• Form 5, Pan Magic Squares    5 x  5, Magic Constant   65, Sudoku Method
  
  
• Form 6, Magic Squares        6 x  6, Magic Constant  111, Medjig Method
  
  
• Form 7, Pan Magic Squares    7 x  7, Magic Constant  175, Sudoku Method
  
  
• Form 8, Most Perfect Msqrs   8 x  8, Magic Constant  260, Binary Method
  
  
• Form 9, Bimagic Squares      9 x  9, Magic Constant  369, Ternary Method
  
  
• Form 12, Most Perfect Msqrs 12 x 12, Magic Constant  870, Basic Pattern Method
  
  
• Form 16, Most Perfect Msqrs 16 x 16, Magic Constant 2056, Basic Pattern Method

Detailed descriptions and instructions are included in the pages referred to above.