|
7.7 Overlapping Sub Squares
7.7.1 Introduction
On Harvey Heinz's site I found following 7th order Magic Square, which contains a 5th order Pan Magic Corner Square (bottom/right)- as described in previous section – and a 3th order Semi Magic Corner Square (top/left corner, only one diagonal summing to 75).
| 22 |
4 |
49 |
48 |
44 |
5 |
3 |
| 46 |
28 |
1 |
2 |
6 |
45 |
47 |
| 7 |
43 |
25 |
30 |
41 |
12 |
17 |
| 36 |
14 |
13 |
19 |
24 |
32 |
37 |
| 8 |
42 |
31 |
39 |
9 |
20 |
26 |
| 35 |
15 |
16 |
27 |
33 |
38 |
11 |
| 21 |
29 |
40 |
10 |
18 |
23 |
34 |
It can be proven that:
-
The application of a Simple Magic 3th order square will require a(17) = a(9) = 25;
-
The application of a Semi Magic 3th order square as shown, will require a(17) = 25 independent from the type of 5th order Magic Square.
Consequently the 5th order square can’t be Symmetric, Ultra Magic, Concentric or Eccentric as described in previous sections.
7.7.2 Analysis
As for the 5th order Corner Square only (Pan) Magic Squares can be used, the full set of equations will be used for the generation of Magic Squares with overlapping sub squares (rather than using the equations of the supplementary rows and columns as a starting point as in Section 7.5.2).
| a(1) |
a(2) |
a(3) |
a(4) |
a(5) |
a(6) |
a(7) |
| a(8) |
a(9) |
a(10) |
a(11) |
a(12) |
a(13) |
a(14) |
| a(15) |
a(16) |
a(17) |
a(18) |
a(19) |
a(20) |
a(21) |
| a(22) |
a(23) |
a(24) |
a(25) |
a(26) |
a(27) |
a(28) |
| a(29) |
a(30) |
a(31) |
a(32) |
a(33) |
a(34) |
a(35) |
| a(36) |
a(37) |
a(38) |
a(39) |
a(40) |
a(41) |
a(42) |
| a(43) |
a(44) |
a(45) |
a(46) |
a(47) |
a(48) |
a(49) |
The defining equations for the Simple Magic Square of the 7th order are:
a( 1) + a( 2) + a( 3) + a( 4) + a( 5) + a( 6) + a( 7) = 175
a( 8) + a( 9) + a(10) + a(11) + a(12) + a(13) + a(14) = 175
a(15) + a(16) + a(17) + a(18) + a(19) + a(20) + a(21) = 175
a(22) + a(23) + a(24) + a(25) + a(26) + a(27) + a(28) = 175
a(29) + a(30) + a(31) + a(32) + a(33) + a(34) + a(35) = 175
a(36) + a(37) + a(38) + a(39) + a(40) + a(41) + a(42) = 175
a(43) + a(44) + a(45) + a(46) + a(47) + a(48) + a(49) = 175
a( 1) + a( 8) + a(15) + a(22) + a(29) + a(36) + a(43) = 175
a( 2) + a( 9) + a(16) + a(23) + a(30) + a(37) + a(44) = 175
a( 3) + a(10) + a(17) + a(24) + a(31) + a(38) + a(45) = 175
a( 4) + a(11) + a(18) + a(25) + a(32) + a(39) + a(46) = 175
a( 5) + a(12) + a(19) + a(26) + a(33) + a(40) + a(47) = 175
a( 6) + a(13) + a(20) + a(27) + a(34) + a(41) + a(48) = 175
a( 7) + a(14) + a(21) + a(28) + a(35) + a(42) + a(49) = 175
a( 1) + a( 9) + a(17) + a(25) + a(33) + a(41) + a(49) = 175
a( 7) + a(13) + a(19) + a(25) + a(31) + a(37) + a(43) = 175
The defining equations for the Pan Magic Corner Square of the 5th order are:
a(17) + a(18) + a(19) + a(20) + a(21) = 125
a(24) + a(25) + a(26) + a(27) + a(28) = 125
a(31) + a(32) + a(33) + a(34) + a(35) = 125
a(38) + a(39) + a(40) + a(41) + a(42) = 125
a(45) + a(46) + a(47) + a(48) + a(49) = 125
a(17) + a(24) + a(31) + a(38) + a(45) = 125
a(18) + a(25) + a(32) + a(39) + a(46) = 125
a(19) + a(26) + a(33) + a(40) + a(47) = 125
a(20) + a(27) + a(34) + a(41) + a(48) = 125
a(21) + a(28) + a(35) + a(42) + a(49) = 125
a(17) + a(25) + a(33) + a(41) + a(49) = 125
a(18) + a(26) + a(34) + a(42) + a(45) = 125
a(19) + a(27) + a(35) + a(38) + a(46) = 125
a(20) + a(28) + a(31) + a(39) + a(47) = 125
a(21) + a(24) + a(32) + a(40) + a(48) = 125
a(21) + a(27) + a(33) + a(39) + a(45) = 125
a(17) + a(28) + a(34) + a(40) + a(46) = 125
a(18) + a(24) + a(35) + a(41) + a(47) = 125
a(19) + a(25) + a(31) + a(42) + a(48) = 125
a(20) + a(26) + a(32) + a(38) + a(49) = 125
The defining equations for the Semi Magic Square of the 3th order are:
a( 1) + a( 2) + a( 3) = 75
a( 8) + a( 9) + a(10) = 75
a(15) + a(16) + a(17) = 75
a( 1) + a( 8) + a(15) = 75
a( 2) + a( 9) + a(16) = 75
a( 3) + a(10) + a(17) = 75
a( 1) + a( 9) + a(17) = 75
The resulting number of equations can be written in matrix representation as:
→ →
A * a = s
which can be reduced, by means of row and column manipulations, and results in following set of linear equations:
a(45) = 125 - a(46) - a(47) - a(48) - a(49)
a(43) = 50 - a(44)
a(39) = 150 - a(40) - a(41) - a(42) - a(47) - a(48)
a(38) = -25 + a(47) + a(48)
a(36) = 50 - a(37)
a(35) = 25 - a(41) - a(42) + a(45) + a(46)
a(34) = 125 - a(40) - a(41) - a(42) - a(48)
a(33) = -25 + a(42) + a(48)
a(32) = a(41) + a(42) - a(46)
a(31) = a(32) + a(40) - a(42) - a(45) + a(46)
a(29) = 50 - a(30)
a(28) = 100 - a(31) - a(34) + a(41) - a(45) - a(46)
a(27) = - a(34) + a(47) + a(49)
a(26) = - a(28) + a(41) + a(48)
a(25) = 125 - a(41) - a(42) - a(48) - a(49)
a(24) = 125 - a(40) - a(41) - a(47) - a(48)
a(23) = 100 - a(30) - a(37) - a(44)
a(22) = 50 - a(23)
a(21) = - a(32) + a(41) + a(47)
a(20) = - a(31) + a(40) + a(46)
a(19) = a(20) - a(40) + a(41) - a(46) + a(49)
a(18) = - a(35) + a(40) + a(48)
a(17) = 25
a(15) = 50 - a(16)
a(13) = a(14) - a(37) + a(42) - a(43) + a(48)
a(11) = 100 - a(12) - a(13) - a(14)
a( 9) = 50 - 0.5 * a(10) - 0.5 * a(16)
a( 8) = 75 - a( 9) - a(10)
a( 7) = 50 - a(14)
a( 6) = 50 - a(13)
a( 5) = 50 - a(12)
a( 4) = 100 - a( 5) - a(6) - a(7)
a( 3) = 50 - a(10)
a( 2) = 50 - a( 8)
a( 1) = 50 - a( 9)
With an optimized guessing routine (MgcSqr7g), based on the equations above, following cases where considered:
-
Case 1: All independant variables constant except a(10) and a(16), which resulted in 8 Magic Squares within 0,63 seconds (ref. Attachment 7.6.1);
-
Case 2: The 5th order Pan Magic - and the 3th order Semi Magic Corner Squares constant, which resulted in 64 Magic Squares within 7,5 seconds (ref. Attachment 7.6.2);
-
Case 3: The border variables, including the 3th order Semi Magic Corner Square constant, which resulted in 72 Magic Squares within 5 hours (ref. Attachment 7.6.3);
-
Case 4: Only the 5th order Pan Magic Square constant, which resulted in 512 Magic Squares within 43,5 seconds (ref. Attachment 7.6.4).
It should be noted that the distinct - partly consecutive - integers for the 5th order Pan Magic Square have been selected from the integers 1 through 49 as shown below (shaded):
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 8 |
9 |
10 |
11 |
12 |
13 |
14 |
| 15 |
16 |
17 |
18 |
19 |
20 |
21 |
| 22 |
23 |
24 |
25 |
26 |
27 |
28 |
| 29 |
30 |
31 |
32 |
33 |
34 |
35 |
| 36 |
37 |
38 |
39 |
40 |
41 |
42 |
| 43 |
44 |
45 |
46 |
47 |
48 |
49 |
Based on these 25 integers, 1152 Pan Magic Squares of the 5th order with corner element 25 can be generated, which was realised with an appropriate guessing routine MgcSqr5a3 within 45 seconds and are shown in Attachment 7.6.5 which includes the 72 Pan Magic Squares found under Case 3 described above.
The number of 7th order Simple Magic Squares which can be constructed based on one 5th order Pan Magic Square depends from the sum s2 of the key variables a(19), a(25) and a(31) and is shown below.
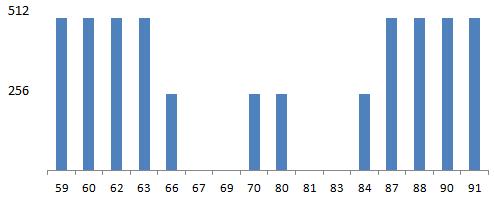
Any of the 16 values of s2 corresponds with 72 Pan Magic Squares of the 5th order (16 * 72 = 1152).
The total number of 7th order Simple Magic Squares with overlapping Sub Squares is 72 * (8 * 512 + 4 * 256) = 368640.
Attachment 7.6.6 shows the first Simple Magic Square of the 7th order found for each of the applicable Pan Magic Squares of the 5th order.
7.7.3 Associated Magic Squares
Order 7 Associated Magic Squares with Overlapping Sub Squares should be composed out of:
-
Two each 4th order Magic Corner Squares A and D (s4 = 100), with the center element in common, and
-
Two each 3th order Semi Magic Corner Squares B and C (s3 = 75).
as shown below.
| a1 |
a2 |
a3 |
a4 |
b1 |
b2 |
b3 |
| a5 |
a6 |
a7 |
a8 |
b4 |
b5 |
b6 |
| a9 |
a10 |
a11 |
a12 |
b7 |
b8 |
b9 |
| a13 |
a14 |
a15 |
a16/d1 |
d2 |
d3 |
d4 |
| c1 |
c2 |
c3 |
d5 |
d6 |
d7 |
d8 |
| c4 |
c5 |
c6 |
d9 |
d10 |
d11 |
d12 |
| c7 |
c8 |
c9 |
d13 |
d14 |
d15 |
d16 |
Associated Magic Squares of order 7 can be constructed based on:
-
One Complementary Pair of order 4 Magic Anti Symmetric Corner Squares and
-
One Complementary Pair of order 3 Semi Magic Anti Symmetric Corner Squares (6 Magic Lines).
A (Semi) Magic Anti Symmetric Square of order n is a (Semi) Magic Square for which:
ai + aj ≠ 2 * sn / n for any i and j (i,j = 1 ... n2; i ≠ j)
The Magic Corner Square A is defined by following linear equations:
a(16) = s4/4
a(13) = s4 - a(14) - a(15) - a(16)
a( 9) = s4 - a(10) - a(11) - a(12)
a( 7) = a( 8) - a(10) + a(12) - a(13) + a(16)
a( 6) = s4 - a( 8) - a(11) - a(12) + a(13) - a(16)
a( 5) = - a( 8) + a(10) + a(11)
a( 4) = s4 - a( 7) - a(10) - a(13)
a( 3) = -s4 - a( 8) + a( 9) + 2*a(10) + 2*a(13) + a(14)
a( 2) = a( 8) - a( 9) - 2*a(10) + a(15) + 2*a(16)
a( 1) = a( 8) + a(12) - a(13)
The Magic Corner Square C is defined by following linear equations:
c(7) = s3 - c(8) - c(9)
c(4) = s3 - c(5) - c(6)
c(3) = - c(6) + c(7) + c(8)
c(2) = s3 - c(5) - c(8)
c(1) = c(5) + c(6) - c(7)
With an optimized guessing routine (MgcSqr7g2), based on the equations above, following cases where considered:
-
Case 1:
The total number of suitable 4th order Anti Symmetric Magic Corner Squares A
has been determined (28800) and is broken down below for i = a(15) = 1 ... 24, 26 ... 49:
| i |
n(i) |
i |
n(i) |
i |
n(i) |
i |
n(i) |
i |
n(i) |
i |
n(i) |
| 1 | 616 |
2 | 712 |
3 | 684 |
4 | 668 |
5 | 656 |
6 | 712 |
| 7 | 744 |
8 | 632 |
9 | 612 |
10 | 576 |
11 | 748 |
12 | 560 |
| 13 | 440 |
14 | 540 |
15 | 596 |
16 | 520 |
17 | 560 |
18 | 624 |
| 19 | 576 |
20 | 456 |
21 | 532 |
22 | 588 |
23 | 508 |
24 | 540 |
| 26 | 540 |
27 | 508 |
28 | 588 |
29 | 532 |
30 | 456 |
31 | 576 |
| 32 | 624 |
33 | 560 |
34 | 520 |
35 | 596 |
36 | 540 |
37 | 440 |
| 38 | 560 |
39 | 748 |
40 | 576 |
41 | 612 |
42 | 632 |
43 | 744 |
| 44 | 712 |
45 | 656 |
46 | 668 |
47 | 684 |
48 | 712 |
49 | 616 |
-
Case 2:
With the first occuring Magic Corner Square A constant, 144 Associated Magic Squares could be generated within 6,5 seconds (ref. Attachment 7.6.7)
The resulting number of Associated Magic Squares appeared to be 4156416 (= 144 * 28800 + 16 * 4 * 144).
Attachment 7.6.8 shows the first 7th order Associated Magic Squares with Overlapping Sub Squares, found for some of the possible 4th order Magic Corner Squares (48 ea).
7.7.4 Spreadsheet Solutions
The linear equations deducted in previous sections, have been applied in following Excel Spread Sheets:
-
CnstrSngl7d1,
Magic Squares of order 7, Overlapping Sub Squares (1)
-
CnstrSngl7d2,
Magic Squares of order 7, Overlapping Sub Squares (2)
Only the red figures have to be “guessed” to construct one of the applicable Magic Squares of the 7th order
(wrong solutions are obvious).
| 