Office Applications and Entertainment, Magic Squares

Vorige Pagina Volgende Pagina Index About the Author

5.4   Further Analysis, Symmetric Magic Squares

In a Symmetric Magic Square, the sum of each pair of elements, which can be connected with a straight line through the centre and which are equidistant to the centre, is 1 + n x n. For 5th order (Pan) Magic Squares these pairs sum to 26.

a(1)

a(2)

a(3)

a(4)

a(5)

a(6)

a(7)

a(8)

a(9)

a(10)

a(11)

a(12)

a(13)

a(14)

a(15)

a(16)

a(17)

a(18)

a(19)

a(20)

a(21)

a(22)

a(23)

a(24)

a(25)

This results in following additional equations:

a( 1) + a(25) = 26
a( 2) + a(24) = 26
a( 7) + a(19) = 26

a( 5) + a(21) = 26
a( 4) + a(22) = 26
a( 9) + a(17) = 26

a( 3) + a(23) = 26
a(10) + a(16) = 26
a( 8) + a(18) = 26

a(11) + a(15) = 26
a(20) + a( 6) = 26
a(12) + a(14) = 26

which can be added to the equations describing either a Magic or a Pan Magic Square of the fifth order.

5.4.1 Associated Magic Squares

When the symmetry conditions are added to the equations describing a Magic Square of the fifth order (Section 3.2), the resulting square - also referred to as Associated Magic Square - is described by following set of linear equations: 

a(21) =     s1     - a(22) - a(23) - a(24) - a(25)
a(16) =     s1     - a(17) - a(18) - a(19) - a(20)
a(15) =     s1 / 5 + a(16) - a(20) + a(21) - a(25)
a(14) =     s1 / 5 + a(17) - a(19) + a(22) - a(24)
a(13) =     s1 / 5
a(12) = 2 * s1 / 5 - a(14)
a(11) = 2 * s1 / 5 - a(15)
a(10) = 2 * s1 / 5 - a(16)
a( 9) = 2 * s1 / 5 - a(17)
a( 8) = 2 * s1 / 5 - a(18)
a( 7) = 2 * s1 / 5 - a(19)
a( 6) = 2 * s1 / 5 - a(20)
a( 5) = 2 * s1 / 5 - a(21)
a( 4) = 2 * s1 / 5 - a(22)
a( 3) = 2 * s1 / 5 - a(23)
a( 2) = 2 * s1 / 5 - a(24)
a( 1) = 2 * s1 / 5 - a(25)

An optimized guessing routine (MgcSqr5c2), counted the 388352 (= 8 * 48544) possible Associated Magic Squares within half an hour, of which the first 744 are shown in Attachment 5.4.2 .

5.4.2 Ultramagic Squares

When the symmetry conditions are added to the equations describing a Pan Magic Square of the fifth order (Section 3.1), the resulting square - also referred to as Ultramagic Square - is described by following set of linear equations: 

a(21) =        s1 - a(22) - a(23) - a(24) - a(25)
a(20) =  0.6 * s1 - a(24) - a(25)
a(19) =  0.6 * s1 + a(22) - a(23) - a(24) - a(25)
a(18) =  0.6 * s1 - a(22) - a(24)
a(17) = -0.4 * s1 + 2 * a(24) + a(25)
a(16) = -0.4 * s1 + a(23) + a(24) + a(25)
a(15) =  0.2 * s1 - a(22) + a(24)
a(14) = -0.8 * s1 + a(23) + 2 * a(24) + 2 * a(25)
a(13) =        s1 / 5
a(12) =    2 * s1 / 5 - a(14)
a(11) =    2 * s1 / 5 - a(15)
a(10) =    2 * s1 / 5 - a(16)
a( 9) =    2 * s1 / 5 - a(17)
a( 8) =    2 * s1 / 5 - a(18)
a( 7) =    2 * s1 / 5 - a(19)
a( 6) =    2 * s1 / 5 - a(20)
a( 5) =    2 * s1 / 5 - a(21)
a( 4) =    2 * s1 / 5 - a(22)
a( 3) =    2 * s1 / 5 - a(23)
a( 2) =    2 * s1 / 5 - a(24)
a( 1) =    2 * s1 / 5 - a(25)

An optimized guessing routine (MgcSqr5c), produced the 128 possible Ultramagic Squares within 18.8 seconds, which are shown in Attachment 5.4.1.

5.4.3 Crosswise Symmetric Magic Squares

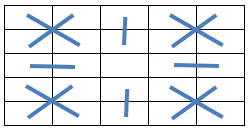
When the equations defining Crosswise Symmetry as illustrated below:


are added to the equations describing a Simple Magic Square of the fifth order (ref. Section 3.2), the resulting Crosswise Symmetric Magic Square is described by following set of linear equations: 

a(21) =      s1     - a(22) - a(23) - a(24) - a(25)
a( 9) =    - s1 / 5 + a(10) + a(15) - a(24) + a(25)
a( 7) = (7 * s1 / 5 - a( 8) - 2*a(10) - a(12) - a(15) + a(21) - a(22) + a(24) - a(25)) / 2
a( 6) =      s1     - a( 7) - a( 8) - a( 9) - a(10)
a(13) =      s1 / 5
a(20) =  2 * s1 / 5 - a(24)
a(19) =  2 * s1 / 5 - a(25)
a(18) =  2 * s1 / 5 - a(23)
a(17) =  2 * s1 / 5 - a(21)
a(16) =  2 * s1 / 5 - a(22)
a(14) =  2 * s1 / 5 - a(15)
a(11) =  2 * s1 / 5 - a(12)
a( 5) =  2 * s1 / 5 - a( 9)
a( 4) =  2 * s1 / 5 - a(10)
a( 3) =  2 * s1 / 5 - a( 8)
a( 2) =  2 * s1 / 5 - a( 6)
a( 1) =  2 * s1 / 5 - a( 7)

An optimized guessing routine (MgcSqr5d2), counted the 388352 (= 8 * 48544) Crosswise Symmetric Squares within 66 seconds, of which the first occuring for a(25) = i (i = 1 ... 12, 14, 15, 16) are shown in Attachment 5.4.3.

5.4.4 Spreadsheet Solutions

The linear equations deducted in previous sections for 5th order Magic Squares, have been applied in following Excel Spread Sheets:

Only the red figures have to be “guessed” to construct one of the applicable Magic Squares (wrong solutions are obvious).

Vorige Pagina Volgende Pagina Index About the Author