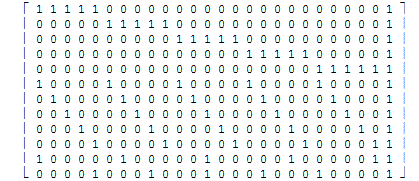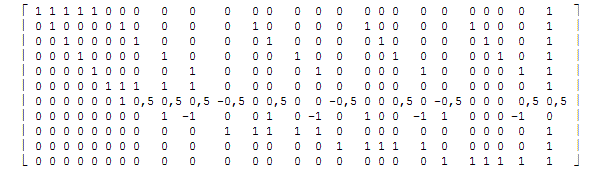Office Applications and Entertainment, Magic Squares

Vorige Pagina Volgende Pagina Index About the Author

3.0   Magic Squares (5 x 5)

3.1   Analytic Solution, Pan Magic Squares

Magic Squares of order 5 can be represented as follows:

a(1)

a(2)

a(3)

a(4)

a(5)

a(6)

a(7)

a(8)

a(9)

a(10)

a(11)

a(12)

a(13)

a(14)

a(15)

a(16)

a(17)

a(18)

a(19)

a(20)

a(21)

a(22)

a(23)

a(24)

a(25)

As the numbers a(i), i = 1 ... 25, in all rows, columns, main - and broken diagonals sum to the same constant this results in following linear equations:

a( 1) + a( 2) + a( 3) + a( 4) + a( 5) = s1
a( 6) + a( 7) + a( 8) + a( 9) + a(10) = s1
a(11) + a(12) + a(13) + a(14) + a(15) = s1
a(16) + a(17) + a(18) + a(19) + a(20) = s1
a(21) + a(22) + a(23) + a(24) + a(25) = s1

a( 1) + a( 6) + a(11) + a(16) + a(21) = s1
a( 2) + a( 7) + a(12) + a(17) + a(22) = s1
a( 3) + a( 8) + a(13) + a(18) + a(23) = s1
a( 4) + a( 9) + a(14) + a(19) + a(24) = s1
a( 5) + a(10) + a(15) + a(20) + a(25) = s1

a( 1) + a( 7) + a(13) + a(19) + a(25) = s1
a( 2) + a( 8) + a(14) + a(20) + a(21) = s1
a( 3) + a( 9) + a(15) + a(16) + a(22) = s1
a( 4) + a(10) + a(11) + a(17) + a(23) = s1
a( 5) + a( 6) + a(12) + a(18) + a(24) = s1

a( 5) + a( 9) + a(13) + a(17) + a(21) = s1
a( 4) + a( 8) + a(12) + a(16) + a(25) = s1
a( 3) + a( 7) + a(11) + a(20) + a(24) = s1
a( 2) + a( 6) + a(15) + a(19) + a(23) = s1
a( 1) + a(10) + a(14) + a(18) + a(22) = s1

Or in matrix representation:

Or shorter:

         →   →
     A * a = s1

The extended matrix of A can be written as:

and reduced, by means of row and column manipulations, to:

which results in the minimum number of linear equations: 

a(21) =  s1 - a(22) - a(23) - a(24) - a(25) 
a(16) =  s1 - a(17) - a(18) - a(19) - a(20) 
a(15) = -0.6 * s1 + a(17) + a(18) + 0.6 * a(21) + 0.6 * a(22) + 0.6 * a(23) + 0.6 * a(24) - 0.4 * a(25)
a(14) =  1.4 * s1 - a(18) - a(19) - a(20) - 0.4 * a(21) - 0.4 * a(22) - 0.4 * a(23) - 1.4 * a(24) - 0.4 * a(25)
a(13) =  1.4 * s1 - a(17) - a(18) - a(19) - 0.4 * a(21) - 0.4 * a(22) - 1.4 * a(23) - 0.4 * a(24) - 0.4 * a(25)
a(12) = -0.6 * s1 + a(19) + a(20) + 0.6 * a(21) - 0.4 * a(22) + 0.6 * a(23) + 0.6 * a(24) + 0.6 * a(25)
a(11) = -0.6 * s1 + a(18) + a(19) - 0.4 * a(21) + 0.6 * a(22) + 0.6 * a(23) + 0.6 * a(24) + 0.6 * a(25)
a(10) =  s1 - a(17) - a(18) - a(22) - a(23)
a( 9) = -s1 + a(18) + a(19) + a(20) + a(23) + a(24) + a(25)
a( 8) = -s1 + a(17) + a(18) + a(19) + a(22) + a(23) + a(24)
a( 7) =  s1 - a(19) - a(20) - a(24) - a(25)
a( 6) =  s1 - a(18) - a(19) - a(23) - a(24)
a( 5) =  0.6 * s1 - a(20) - 0.6 * a(21) + 0.4 * a(22) + 0.4 * a(23) - 0.6 * a(24) - 0.6 * a(25)
a( 4) =  0.6 * s1 - a(19) + 0.4 * a(21) + 0.4 * a(22) - 0.6 * a(23) - 0.6 * a(24) - 0.6 * a(25)
a( 3) =  0.6 * s1 - a(18) + 0.4 * a(21) - 0.6 * a(22) - 0.6 * a(23) - 0.6 * a(24) + 0.4 * a(25)
a( 2) =  0.6 * s1 - a(17) - 0.6 * a(21) - 0.6 * a(22) - 0.6 * a(23) + 0.4 * a(24) + 0.4 * a(25)
a( 1) = -1.4 * s1 + a(17) + a(18) + a(19) + a(20) + 0.4 * a(21) + 0.4 * a(22) + 1.4 * a(23) + 1.4 * a(24) + 0.4 * a(25)

which can can be rewritten as:

a(21) =  s1 - a(22) - a(23) - a(24) - a(25)
a(16) =  s1 - a(17) - a(18) - a(19) - a(20)
a(15) =       a(17) + a(18) - a(25)
a(14) =  s1 - a(18) - a(19) - a(20) - a(24)
a(13) =  s1 - a(17) - a(18) - a(19) - a(23)
a(12) =       a(19) + a(20) - a(22)
a(11) =       a(18) + a(19) - a(21)
a(10) =  s1 - a(17) - a(18) - a(22) - a(23)
a( 9) =  s1 - a(16) - a(17) - a(21) - a(22)
a( 8) =  s1 - a(16) - a(20) - a(21) - a(25)
a( 7) =  s1 - a(19) - a(20) - a(24) - a(25)
a( 6) =  s1 - a(18) - a(19) - a(23) - a(24)
a( 5) =     - a(20) + a(22) + a(23)
a( 4) =     - a(19) + a(21) + a(22)
a( 3) =     - a(18) + a(21) + a(25)
a( 2) =     - a(17) + a(24) + a(25)
a( 1) =     - a(16) + a(23) + a(24)

The linear equations shown above, are ready to be solved, for the magic constant 65.

The solutions can be obtained by guessing a(17), a(18), a(19), a(20), a(22), a(23), a(24) and a(25) and filling out these guesses in the abovementioned equations.

For distinct integers also following inequalities should be applied:

0 < a(i) =< 25        for i = 1, 2, ... 16, 21
a(i) ≠ a(j)           for i ≠ j

which can be incorporated in the guessing routine and reduce the number of guesses, and consequently the processor time, dramatically (MgcSqr5a).

The 28800 solutions of the 5th order Pan Magic Squares, for integers from 1 to 25 and related magic constant 65, are available in Attachment 5.2.6 and were generated within 20 minutes.

However, as this method will become slower and slower for higher order magic squares it might be wise to reconsider the method of solving these equations.

3.2.1 Analytic Solution, Simple Magic Squares (1)

If the requirements for Pan Magic Squares, as discussed in section 3.1 above, are moderated till the sum of all rows, columns and main diagonals sum to the same magic constant, the applicable equations are:

a( 1) + a( 2) + a( 3) + a( 4) + a( 5) = s1
a( 6) + a( 7) + a( 8) + a( 9) + a(10) = s1
a(11) + a(12) + a(13) + a(14) + a(15) = s1
a(16) + a(17) + a(18) + a(19) + a(20) = s1
a(21) + a(22) + a(23) + a(24) + a(25) = s1

a( 1) + a( 6) + a(11) + a(16) + a(21) = s1
a( 2) + a( 7) + a(12) + a(17) + a(22) = s1
a( 3) + a( 8) + a(13) + a(18) + a(23) = s1
a( 4) + a( 9) + a(14) + a(19) + a(24) = s1
a( 5) + a(10) + a(15) + a(20) + a(25) = s1

a( 1) + a( 7) + a(13) + a(19) + a(25) = s1

a( 5) + a( 9) + a(13) + a(17) + a(21) = s1

Or in matrix representation:

Or shorter:

         →   →
     A * a = s1

The extended matrix of A can be written as:

and reduced, by means of row and column manipulations, to:

which results in the minimum number of linear equations: 

a(21) =  65 - a(22) - a(23) - a(24) - a(25)
a(16) =  65 - a(17) - a(18) - a(19) - a(20)
a(11) =  65 - a(12) - a(13) - a(14) - a(15)
a( 9) =       a(10) - a(13) + a(15) - a(17) + a(20) - a(21) + a(25)
a( 7) = (65 - a( 8) - a( 9) - a(10) + a(11) - a(13) + a(16) - a(19) + a(21) - a(25)) / 2
a( 6) =  65 - a( 7) - a( 8) - a( 9) - a(10)
a( 5) =  65 - a( 9) - a(13) - a(17) - a(21)
a( 4) =  65 - a( 9) - a(14) - a(19) - a(24)
a( 3) =  65 - a( 8) - a(13) - a(18) - a(23)
a( 2) =  65 - a( 7) - a(12) - a(17) - a(22)
a( 1) =  65 - a( 2) - a( 3) - a( 4) - a( 5)

The linear equations shown above, are ready to be solved, for the magic constant 65.

The solutions can be obtained by guessing a(8), a(10), a(12) ... a(15), a(17) ... a(20) and a(22) ... a(25) and filling out these guesses in the abovementioned equations.

For distinct integers also following inequalities should be applied:

0 < a(i) =< 25        for i = 1, 2 ... 7, 9, 11, 16 and 21
Int(a(i)) = a(i)      for i = 7
a(i) ≠ a(j)           for i ≠ j

which can be incorporated in the guessing routine (MgcSqr5a2).

With the variables a(20) thru a(25) constant subject guessing routine generated 728 Simple Magic Squares of the 5th order within 13,5 minutes, which are shown in Attachment 3.4.1.

3.2.2 Analytic Solution, Simple Magic Squares (2)

Although this result might look satisfactorily, it is disappointing with regard to the total number of Simple Magic Squares of the 5th order (8 * 275305224) as determined by Richard Schroeppel in 1973 (ref. Scientific American 1978).

A faster routine - in which after the main diagonals the remaining rows and columns are calculated - can be developed.

This sequence together with the properties of a Simple Magic Square result, after deduction, in following set of linear equations:

a( 1) = s1 - a( 7) - a(13) - a(19) - a(25)
a( 5) = s1 - a( 9) - a(13) - a(17) - a(21)
a( 6) = s1 - a( 7) - a( 8) - a( 9) - a(10)
a(16) = s1 - a(21) - a(11) - a( 6) - a( 1)
a(20) = s1 - a(25) - a(15) - a(10) - a( 5)
a(18) = s1 - a(16) - a(17) - a(19) - a(20)
a(12) = s1 - a(11) - a(13) - a(14) - a(15)
a(23) = s1 - a( 3) - a( 8) - a(13) - a(18)
a(22) = s1 - a( 2) - a( 7) - a(12) - a(17)
a( 4) = s1 - a( 1) - a( 2) - a( 3) - a( 5)
a(24) = s1 - a(21) - a(22) - a(23) - a(25)

The solutions can be obtained by guessing the 14 parameters:

   a(i) for i = 2, 3, 7, 8, 9, 10, 11, 13, 14, 15, 17, 19, 21, 25

and filling out these guesses in the abovementioned equations.

The linear equations shown above can be incorporated in a guessing routine, in which the relations ensuring Unique Essential Different Simple Magic Squares:

a(25) < a(19), a(7), a(1), a(21), a(17), a(9), a(5)
a(19) < a(7) and a(21) < a(5)

can be incorporated (MgcSqr5b2).

With the diagonal a(1) - a(25) constant, subject routine generated 5111 Unique Simple Magic Squares of the 5th order within 17,3 seconds, of which the first 728 are shown in Attachment 3.4.2.

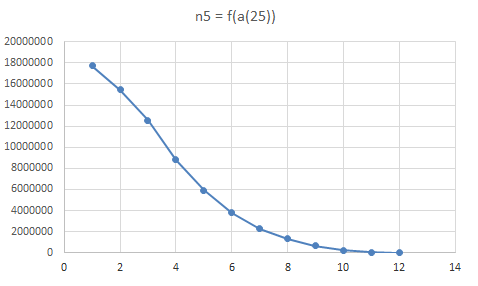
The same routine counted 68826306 (= 275305224/4) Essential Different Simple Magic Squares in 18,4 hrs, thus confirming the findings of Richard Schroeppel:

Unique Borders

Attachment 3.4.3 shows the frequency n5 of subject Essential Different Magic Squares as a function of a(25) and a(19).

3.3   Other Magic Constants

Other magic constants are possible for both Magic Squares and Pan Magic Squares.

Magic Squares of the 5th order with magic constant 315 for distinct integers from 1 to 125, can be generated:

  • either with procedure MgcSqr5a2, based on the equations developed in Section 3.2 above (slow);

  • or with the procedure described in Section 3.6.3 below (fast, but not all possible solutions).

The last mentioned procedure (CnstrSqrs5b) counted in about 24 hours 10310400 Pan Magic Squares of the 5th order with magic constant 315 for distinct integers from 1 to 125.

The importance of 5th order (Pan) Magic Squares with Magic Constant 315 will become clear in Section 5.4 of 'Magic Cubes'.

3.4   Rotation, Reflection, Row and Column Shifts

Rotation and Reflection (General)

Each Magic Square has 8 orientations which can be reached by means of rotation and/or reflection (ref. Attachment 5.5.2).

Row and Column Shifts (Pan Magic)

Each Pan Magic Square of order n is part of a collection of n x n Pan Magic Squares which can be obtained by means of row and/or column shifts (ref. Attachment 5.5.5).

Combined Rotation, Reflection, Row and Column Shifts (Pan Magic)

Consequently each Pan Magic Square of order n is part of a collection {Aijk} containing 8 x n x n Pan Magic Squares (ref. Attachment 5.5.5).

3.5   Transformations and Standard Positions

3.5.1 Transformations

Each 5th order Simple Magic Square corresponds with 4 transformations as described below:

  • A permutation can be applied to the lines 1, 2 provided that the same permutation is applied to the lines 5, 4 (ref. Attachment 5.5.3).

  • Any line n can be interchanged with line (6 - n), as well as the combination of these two permutations, resulting in 4 transformations (ref. Attachment 5.5.3).
    It should be noted that for each square the 180o rotated aspect is included in this collection.

  • The resulting number of transformations is 2 * 4 = 8, however with only four unique solutions (ref. Attachment 5.5.3).

Note: Secondary properties, e.g. pandiagonal, are not invariant to the transformations described above.

Based on the 4 unique transformations and the eight squares which can be found by means of rotation and/or reflection any 5th order Simple Magic Square corresponds with a Class of 4 * 8 = 32 Magic Squares (ref. Attachment 5.5.6).

3.5.2 Standard Positions

Standard Position of Unique Magic Squares

Each of the 8 orientations (aspects) can be considered to be the same Unique Magic Square.

The standard Position of Unique Magic Squares is defined by the four corners:

a(25) < a(21), a(5), a(1)
a(21) < a(5)

Standard position of Essential Different Magic Squares

Two different Unique Magic Squares are called Essential Different, if it is not possible to transform one square into the other square by means of the transformations described above.

The standard position of Essential Different Magic Squares is defined by the integers of the two main diagonals:

a(25) < a(19), a(7), a(1), a(21), a(17), a(9), a(5)
a(19) < a(7) and a(21) < a(5)

An example of a square in standard position - with the main diagonals highlighted - is shown in Attachment 5.5.6.

Vorige Pagina Volgende Pagina Index About the Author