Office Applications and Entertainment, Magic Cubes

3.4 Construction based on Pan Magic Squares

Almost Perfect Magic Cubes of order 4 can be constructed by means of following method:

1. Construct a Sudoku Comparable Cube C, such that every row, column, pillar and space diagonal contain the numbers
   0, 1, 2 and 3 for which also the plane diagonals sum to 6.
   
   
2. Construct, based on a Pan Magic Square P of the 4^th order, a cube B such that:
   
   Plane B1 = P, Plane B2 thru B4 are deducted from P as shown below.
   All 12 orthogonal planes of the resulting cube B are Pan Magic.
   
   

3. Construct a cube A by adding 16 times the value of each element of C to each corresponding element of B.
   The resulting cube A is a Non Symmetrical Almost Perfect Magic Cube.

   B1 = Pan Magic p11 p12 p13 p14 p21 p22 p23 p24 p31 p32 p33 p34 p41 p42 p43 p44	C1 1 0 3 2 0 2 1 3 3 1 2 0 2 3 0 1	A1 p11+16 p12 p13+3*16 p14+2*16 p21 p22+2*16 p23+16 p24+3*16 p31+3*16 p32+16 p33+2*16 p34 p41+2*16 p42+3*16 p43 p44+16
   B2 p22 p21 p24 p23 p12 p11 p14 p13 p42 p41 p44 p43 p32 p31 p34 p33	C2 0 2 1 3 2 3 0 1 1 0 3 2 3 1 2 0	A2 p22 p21+2*16 p24+16 p23+3*16 p12+2*16 p11+3*16 p14 p13+16 p42+16 p41 p44+3*16 p43+2*16 p32+3*16 p31+16 p34+2*16 p33
   B3 p33 p34 p31 p32 p43 p44 p41 p42 p13 p14 p11 p12 p23 p24 p21 p22	C3 3 1 2 0 1 0 3 2 2 3 0 1 0 2 1 3	A3 p33+3*16 p34+16 p31+2*16 p32 p43+16 p44 p41+3*16 p42+2*16 p13+2*16 p14+3*16 p11 p12+16 p23 p24+2*16 p21+16 p22+3*16
   B4 p44 p43 p42 p41 p34 p33 p32 p31 p24 p23 p22 p21 p14 p13 p12 p11	C4 2 3 0 1 3 1 2 0 0 2 1 3 1 0 3 2	A4 p44+2*16 p43+3*16 p42 p41+16 p34+3*16 p33+16 p32+2*16 p31 p24 p23+2*16 p22+16 p21+3*16 p14+16 p13 p12+3*16 p11+2*16

Sudoku Comparable Cubes as described above can be obtained by applying the same equations as deducted in Section 3.2.2, however for a Magic Sum 6 and with the less strict restriction that the elements of each row, column, pillar and space diagonal should be different.

An optimized guessing routine (SudCube4) produced 8 cubes within 1,75 seconds, which are shown in Attachment 3.5.1.

It should be noted that Cube 8, 7, 6 and 5 can be obtained by means of reflection (left to right) of Cube 1, 2, 3 and 4.

The rows, columns and plane diagonals of Cube A sum to the corresponding sum of Pan Magic Square P plus 16 times the corresponding sum of the Sudoku Cube C which results in s1 = 34 + 16 * 6 = 130.

A numerical example is shown below:

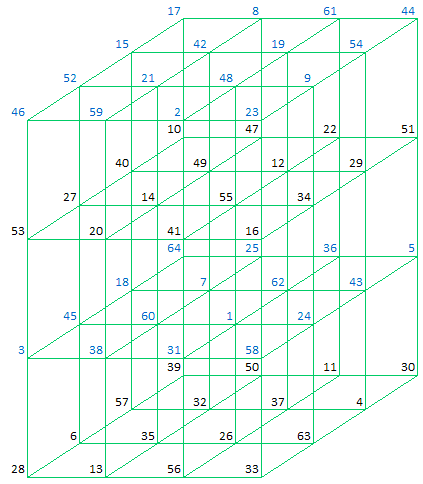
The 8 Almost Perfect Magic Cubes which can be found for Pan Magic Square B1 and each of the possible Sudoku Comparable Cubes are shown in Attachment 3.5.2.

If the corresponding Classes are compared, it appears - as expected - that only four Classes contain different cubes.

Consequently of the Sudoku Comparable Cubes shown in Attachment 3.5.1 only the ones which can't be obtained by means of rotation or reflection of each other can be used (highlighted in blue).

An optimized guessing routine (MgcCube4b), produced the 384 possible Almost Perfect Magic Cubes for the Sudoku Comparable Cube shown above in 66 seconds, which are shown in Attachment 3.5.3 and further referred to as Collection {B}.

However not all elements of Collection {B} will result in a unique Class as defined in Section 3.1.

If the first cube of collection {B} is used as a Base Cube, the resulting Class (ref. Attachment 3.5.4) will contain
7 other elements of {B} (highlighted in red), due to the method the cubes of {B} have been constructed.

These 7 cubes should be excluded from the collection of possible Base Cubes. Continuing like this, a collection of 48
(= 384/8) possible Base Cubes will remain (ref. Attachment 3.5.5).

Consequently, based on the method described above, 48 * 48 = 2304 Almost Perfect Magic Cubes can be constructed for each of the 4 Sudoku Comparable Cubes.

It should be noted that, although quite fast, only a small portion of all possible Almost Perfect Magic Cubes can be constructed with this method.

3.5 Interactve Solution

The construction method described in Section 3.4 above has been applied in following Interactive Solution:

	Select B1 H1a H1b H2a H2b V1a V1b V2a V2b 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 Select C1 S1 S2 S3 S4	B1 C1 A1 B2 C2 A2 B3 C3 A3 B4 C4 A4

Procedure:

1. Select 4 Binaries out of the pairs H1a/H1b, H2a/H2b, V1a/V1b and V2a/V2b with the 4 upper left selection buttons.
   
   
2. Select a sequence (1, 2 ... 24) for the four selected Binaries with the selection button left of the button ‘Sqr B1’ and confirm by pushing button 'SqrB1' (for details regarding solutions based on Binary Matrices refer to Form4b).
   
   
3. Select one of the Sudoku Comparable Cubes with the lower left selection button, and confirm by pushing button 'SqrC1'.
   
   
4. Press the button ‘Calculate’ to calculate and visualise the resulting Magic Cube A of the 4^th order. Press the button ‘Show 3d’ to visualise the constructed cube in 3d view.

Have Fun!