Office Applications and Entertainment, Magic Cubes

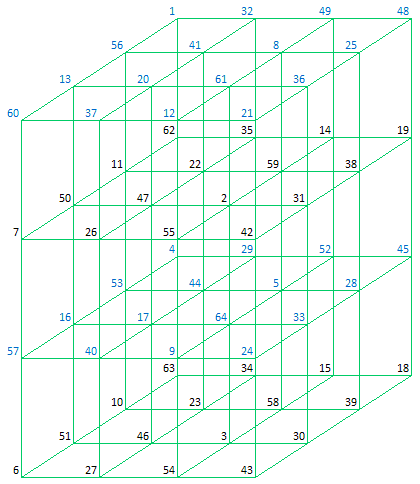
3.7   Pantriagonal Magic Cubes (4 x 4 x 4)

3.7.1 Historical Background

Magic Cubes as discussed in Section 2.1 for which basically only the rows, columns, pillars and 4 space diagonals (main triagonals) sum to the Magic Constant are normally referred to as Simple Magic Cubes.

John Hendricks introduced the concept of Pantriagonal Magic Cubes, being Simple Magic Cubes for which all main and broken triagonals sum to the Magic Constant.

In 1972 he published a 4^th order Pantriagonal Magic Cube, which is shown below together with the 12 orthogonal planes:

The cube shown above has following additional properties:

1. Compact : Every 2 x 2 sub square in each of the orthogonal planes sums to the Magic Constant.
   
   
2. Complete: Every (pan)triagonal contains n/2 complementary pairs spaced n/2 apart along the (pan)triagonal.
             Comparable with Most Perfect Magic Squares as discussed in 'Magic Squares', Section 2.4).

As a consequence of the defining properties mentioned above, the cube has also following properties:

3. Every 2 x 2 x 2 block of cells (including wrap-around) sums to n*(n³ + 1) = 260 (Cubic Compact).
   
   
4. The corners of all Sub-Cubes of orders 3 sum to n*(n³ + 1) = 260.

A Pantriagonal Magic Cube can be transformed into another Pantriagonal Magic Cube by moving an orthogonal plane from one side of the cube to the other. (Comparable with the row and column movements for Pandiagonal Magic Squares as discussed in 'Magic Squares' Section 3.4).

Consequently a Pantriagonal Magic Cube belongs to a collection {A_ijk^m} of 4³ * 48 = 3072 elements which can be found by means of rotation, reflection or plane movements.

The Class of 48 elements which can be obtained by rotation / reflection of a Pantriagonal Cube is shown in Attachment 3.7.1.

The Class of 64 elements which can be obtained by planar shifts of a Pantriagonal Cube is shown in Attachment 3.7.2. Each cube of Attachment 3.7.1 can be used as a Base for Attachment 3.7.2.

It should be noted that the planar shifts are from left to right (L1, L2, L3), from back to front (B1, B2, B3) and from bottom to top (T1, T2, T3).

3.7.2 Analytic Solution

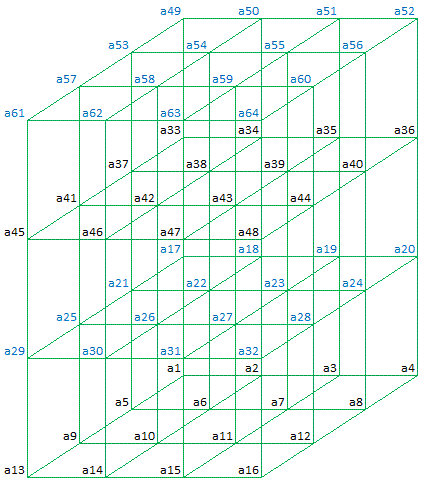
In general Magic Cubes of order 4 can be represented as follows:

As all 2 x 2 squares in each of the orthogonal planes sum to 130 and all complementary pairs of all (pan)triagonals sum to 65, this results in linear equations like:

The equations for the other orthogonal planes and pantriagonals are comparable.

The complete set of equations results, after deduction, in following set of linear equations describing the "Pantriagonal Magic Cubes" as published by John Hendricks:

a(61) =  130 - a(62) - a(63) - a(64)
a(59) =  130 - a(60) - a(63) - a(64)
a(58) =        a(60) - a(62) + a(64)
a(57) =      - a(60) + a(62) + a(63)
a(55) =      - a(56) + a(63) + a(64)
a(54) =        a(56) + a(62) - a(64)
a(53) =  130 - a(56) - a(62) - a(63)
a(52) =  130 - a(56) - a(60) - a(64)
a(51) =        a(56) + a(60) - a(63)
a(50) =  130 - a(56) - a(60) - a(62)
a(49) = -130 + a(56) + a(60) + a(62) + a(63) + a(64)
a(47) =  130 - a(48) - a(63) - a(64)
a(46) =        a(48) - a(62) + a(64)
a(45) =      - a(48) + a(62) + a(63)
a(44) =  130 - a(48) - a(60) - a(64)
a(43) = -130 + a(48) + a(60) + a(63) + 2 * a(64)
a(42) =  130 - a(48) - a(60) + a(62) - 2 * a(64)
a(41) =        a(48) + a(60) - a(62) - a(63) + a(64)
a(40) =        a(48) - a(56) + a(64)
a(39) =  130 - a(48) + a(56) - a(63) - 2 * a(64)
a(38) =        a(48) - a(56) - a(62) + 2 * a(64)
a(37) =      - a(48) + a(56) + a(62) + a(63) - a(64)
a(36) =      - a(48) + a(56) + a(60)
a(35) =        a(48) - a(56) - a(60) + a(63) + a(64)
a(34) =      - a(48) + a(56) + a(60) + a(62) - a(64)
a(33) =  130 + a(48) - a(56) - a(60) - a(62) - a(63)
a(32) =   65 - a(56) - a(62) + a(64)
a(31) = - 65 + a(56) + a(62) + a(63)
a(30) =   65 - a(56)
a(29) =   65 + a(56) - a(63) - a(64)
a(28) = - 65 + a(56) + a(60) + a(62)
a(27) =  195 - a(56) - a(60) - a(62) - a(63) - a(64)
a(26) = - 65 + a(56) + a(60) + a(64)
a(25) =   65 - a(56) - a(60) + a(63)
a(24) =   65 - a(62)
a(23) = - 65 + a(62) + a(63) + a(64)
a(22) =   65 - a(64)
a(21) =   65 - a(63)
a(20) =   65 - a(60) + a(62) - a(64)
a(19) =   65 + a(60) - a(62) - a(63)
a(18) =   65 - a(60)
a(17) = - 65 + a(60) + a(63) + a(64)
a(16) =   65 - a(48) + a(56) + a(62) - 2 * a(64)
a(15) =   65 + a(48) - a(56) - a(62) - a(63) + a(64)
a(14) =   65 - a(48) + a(56) - a(64)
a(13) = - 65 + a(48) - a(56) + a(63) + 2 * a(64)
a(12) =   65 + a(48) - a(56) - a(60) - a(62) + a(64)
a(11) = - 65 - a(48) + a(56) + a(60) + a(62) + a(63)
a(10) =   65 + a(48) - a(56) - a(60)
a( 9) =   65 - a(48) + a(56) + a(60) - a(63) - a(64)
a( 8) =   65 - a(48) + a(62) - a(64)
a( 7) =   65 + a(48) - a(62) - a(63)
a( 6) =   65 - a(48)
a( 5) = - 65 + a(48) + a(63) + a(64)
a( 4) = - 65 + a(48) + a(60) - a(62) + 2 * a(64)
a( 3) =   65 - a(48) - a(60) + a(62) + a(63) - a(64)
a( 2) = - 65 + a(48) + a(60) + a(64)
a( 1) =  195 - a(48) - a(60) - a(63) - 2 * a(64)

The linear equations shown above, are ready to be solved, for the Magic Constant 130.

The solutions can be obtained by guessing:

   a(48), a(56), a(60), a(62) ... a(64)

and filling out these guesses in the abovementioned equations.

For distinct integers also following relations are applicable:

0 < a(i) =< 64        for i = 1, 2 ... 47, 49 ... 55, 57 ... 59, 61
a(i) ≠ a(j)           for i ≠ j

which have been incorporated in an optimized guessing routine (MgcCube4d).

Subject guessing routine produced 64 * 6 * 120 = 46080 Pantriagonal Magic Cubes within 45 minutes, of which the first 120 are shown in Attachment 3.7.3.

An alternative method to generate Pantriagonal Magic Cubes, based on the equations deducted above, will be discussed in Section 3.12.4.