Office Applications and Entertainment, Magic Cubes

Vorige Pagina Volgende Pagina Index About the Author

4.0 Magic Cubes (5 x 5 x 5)

4.1 Historical Background

Until 2003 it was thought that Perfect Magic Cubes of the 5th order don’t exist.

However in 2003 Walter Trump and Christian Boyer constructed the Perfect Magic Cube of the 5th order shown below:

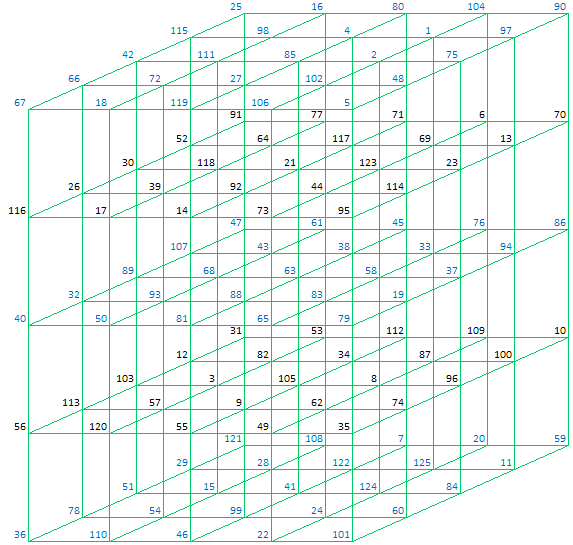
Magic Cube, Walter Trump (2003)

Plane 11 (Top)

25 16 80 104 90
115 98 4 1 97
42 111 85 2 75
66 72 27 102 48
67 18 119 106 5

Plane 12

91 77 71 6 70
52 64 117 69 13
30 118 21 123 23
26 39 92 44 114
116 17 14 73 95

Plane 13

47 61 45 76 86
107 43 38 33 94
89 68 63 58 37
32 93 88 83 19
40 50 81 65 79

Plane 14

31 53 112 109 10
12 82 34 87 100
103 3 105 8 96
113 57 9 62 74
56 120 55 49 35

Plane 15

121 108 7 20 59
29 28 122 125 11
51 15 41 124 84
78 54 99 24 60
36 110 46 22 101


The cube contains all numbers 1 to 125. All 25 rows, 25 columns, 25 pillars, 30 diagonals and 4 space diagonals sum to
the Magic Constant 315.

The cube belongs to a Class of 48 elements which can be found by means of rotation and/or reflection which is visualised in Attachment 4.1.

For Magic Cubes of the 5th order it has been proven that Bordered Perfect Magic Cubes and Perfect Central Symmetric Magic Cubes don’t exist.

4.2a Analytic Solution, Perfect Magic Cubes

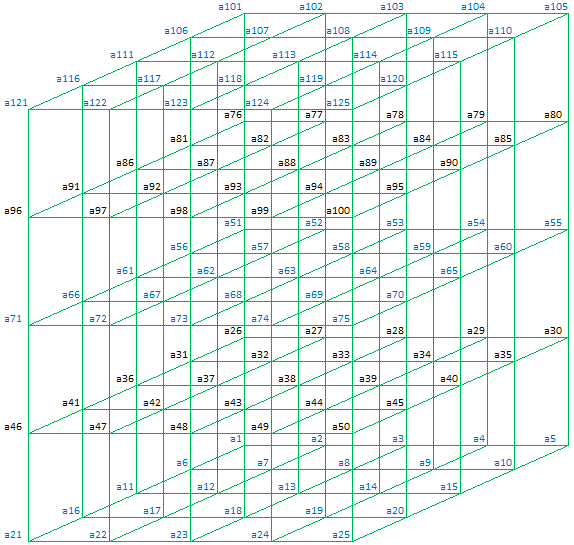
In general Magic Cubes of order 5 can be represented as follows:

Magic Cube (5 x 5 x 5)

Plane 11 (Top)

a101 a102 a103 a104 a105
a106 a107 a108 a109 a110
a111 a112 a113 a114 a115
a116 a117 a118 a119 a120
a121 a122 a123 a124 a125

Plane 12

a76 a77 a78 a79 a80
a81 a82 a83 a84 a85
a86 a87 a88 a89 a90
a91 a92 a93 a94 a95
a96 a97 a98 a99 a100

Plane 13

a51 a52 a53 a54 a55
a56 a57 a58 a59 a60
a61 a62 a63 a64 a65
a66 a67 a68 a69 a70
a71 a72 a73 a74 a75

Plane 14

a26 a27 a28 a29 a30
a31 a32 a33 a34 a35
a36 a37 a38 a39 a40
a41 a42 a43 a44 a45
a46 a47 a48 a49 a50

Plane 15

a1 a2 a3 a4 a5
a6 a7 a8 a9 a10
a11 a12 a13 a14 a15
a16 a17 a18 a19 a20
a21 a22 a23 a24 a25


As the numbers a(i), i = 1 ... 125 for each of the rows, columns, pillars, diagonals and space diagonals sum to the Magic Constant (315) this results in following linear equations:

Rows:

a101 + a102 + a103 + a104 + a105 = 315
a106 + a107 + a108 + a109 + a110 = 315
a111 + a112 + a113 + a114 + a115 = 315
a116 + a117 + a118 + a119 + a120 = 315
a121 + a122 + a123 + a124 + a125 = 315

a76  + a77  + a78  + a79  + a80  = 315
a81  + a82  + a83  + a84  + a85  = 315
a86  + a87  + a88  + a89  + a90  = 315
a91  + a92  + a93  + a94  + a95  = 315
a96  + a97  + a98  + a99  + a100 = 315

a51  + a52  + a53  + a54  + a55  = 315
a56  + a57  + a58  + a59  + a60  = 315
a61  + a62  + a63  + a64  + a65  = 315
a66  + a67  + a68  + a69  + a70  = 315
a71  + a72  + a73  + a74  + a75  = 315

a26  + a27  + a28  + a29  + a30  = 315
a31  + a32  + a33  + a34  + a35  = 315
a36  + a37  + a38  + a39  + a40  = 315
a41  + a42  + a43  + a44  + a45  = 315
a46  + a47  + a48  + a49  + a50  = 315

a1   + a2   + a3   + a4   + a5   = 315
a6   + a7   + a8   + a9   + a10  = 315
a11  + a12  + a13  + a14  + a15  = 315
a16  + a17  + a18  + a19  + a20  = 315
a21  + a22  + a23  + a24  + a25  = 315

Plane Diagonals:

a101 + a107 + a113 + a119 + a125 = 315
a105 + a109 + a113 + a117 + a121 = 315
a76  + a82  + a88  + a94  + a100 = 315
a80  + a84  + a88  + a92  + a96  = 315
a51  + a57  + a63  + a69  + a75  = 315
a55  + a59  + a63  + a67  + a71  = 315
a26  + a32  + a38  + a44  + a50  = 315
a30  + a34  + a38  + a42  + a46  = 315
a1   + a7   + a13  + a19  + a25  = 315
a5   + a9   + a13  + a17  + a21  = 315

Space Diagonals:

a21  + a42  + a63  + a84  + a105 = 315
a25  + a44  + a63  + a82  + a101 = 315
a5   + a34  + a63  + a92  + a121 = 315
a1   + a32  + a63  + a94  + a125 = 315

Columns:

a101 + a106 + a111 + a116 + a121 = 315
a102 + a107 + a112 + a117 + a122 = 315
a103 + a108 + a113 + a118 + a123 = 315
a104 + a109 + a114 + a119 + a124 = 315
a105 + a110 + a115 + a120 + a125 = 315

a76  + a81  + a86  + a91  + a96  = 315
a77  + a82  + a87  + a92  + a97  = 315
a78  + a83  + a88  + a93  + a98  = 315
a79  + a84  + a89  + a94  + a99  = 315
a80  + a85  + a90  + a95  + a100 = 315

a51  + a56  + a61  + a66  + a71  = 315
a52  + a57  + a62  + a67  + a72  = 315
a53  + a58  + a63  + a68  + a73  = 315
a54  + a59  + a64  + a69  + a74  = 315
a55  + a60  + a65  + a70  + a75  = 315

a26  + a31  + a36  + a41  + a46  = 315
a27  + a32  + a37  + a42  + a47  = 315
a28  + a33  + a38  + a43  + a48  = 315
a29  + a34  + a39  + a44  + a49  = 315
a30  + a35  + a40  + a45  + a50  = 315

a1   + a6   + a11  + a16  + a21  = 315
a2   + a7   + a12  + a17  + a22  = 315
a3   + a8   + a13  + a18  + a23  = 315
a4   + a9   + a14  + a19  + a24  = 315
a5   + a10  + a15  + a20  + a25  = 315



a105 + a79  + a53  + a27  + a1   = 315
a101 + a77  + a53  + a29  + a5   = 315
a110 + a84  + a58  + a32  + a6   = 315
a106 + a82  + a58  + a34  + a10  = 315
a115 + a89  + a63  + a37  + a11  = 315
a111 + a87  + a63  + a39  + a15  = 315
a120 + a94  + a68  + a42  + a16  = 315
a116 + a92  + a68  + a44  + a20  = 315
a125 + a99  + a73  + a47  + a21  = 315
a121 + a97  + a73  + a49  + a25  = 315


Pillars:

a101 + a76  + a51 + a26 + a1  = 315
a102 + a77  + a52 + a27 + a2  = 315
a103 + a78  + a53 + a28 + a3  = 315
a104 + a79  + a54 + a29 + a4  = 315
a105 + a80  + a55 + a30 + a5  = 315

a106 + a81  + a56 + a31 + a6  = 315
a107 + a82  + a57 + a32 + a7  = 315
a108 + a83  + a58 + a33 + a8  = 315
a109 + a84  + a59 + a34 + a9  = 315
a110 + a85  + a60 + a35 + a10 = 315

a111 + a86  + a61 + a36 + a11 = 315
a112 + a87  + a62 + a37 + a12 = 315
a113 + a88  + a63 + a38 + a13 = 315
a114 + a89  + a64 + a39 + a14 = 315
a115 + a90  + a65 + a40 + a15 = 315

a116 + a91  + a66 + a41 + a16 = 315
a117 + a92  + a67 + a42 + a17 = 315
a118 + a93  + a68 + a43 + a18 = 315
a119 + a94  + a69 + a44 + a19 = 315
a120 + a95  + a70 + a45 + a20 = 315

a121 + a96  + a71 + a46 + a21 = 315
a122 + a97  + a72 + a47 + a22 = 315
a123 + a98  + a73 + a48 + a23 = 315
a124 + a99  + a74 + a49 + a24 = 315
a125 + a100 + a75 + a50 + a25 = 315



a105 + a85  + a65  + a45  + a25 = 315
a125 + a95  + a65  + a35  + a5  = 315
a104 + a84  + a64  + a44  + a24 = 315
a124 + a94  + a64  + a34  + a4  = 315
a103 + a83  + a63  + a43  + a23 = 315
a123 + a93  + a63  + a33  + a3  = 315
a102 + a82  + a62  + a42  + a22 = 315
a122 + a92  + a62  + a32  + a2  = 315
a101 + a81  + a61  + a41  + a21 = 315
a121 + a91  + a61  + a31  + a1  = 315

As a result of the construction method used by Walter Trump, there are many symmetries present in this cube which can be covered by following additional equations:

Center Pillars:
a7  + a107 = 126
a8  + a108 = 126
a9  + a109 = 126
a12 + a112 = 126
a13 + a113 = 126
a14 + a114 = 126
a17 + a117 = 126
a18 + a118 = 126
a19 + a119 = 126

Space Diagonals:
a1   + a125 = 126
a5   + a121 = 126

Inner Cube:
Center Pillar:
a38 + a88 = 126

Plane 13:

a51 + a75 = 126
a52 + a74 = 126
a53 + a73 = 126
a54 + a72 = 126
a55 + a71 = 126
a56 + a70 = 126
a60 + a66 = 126
a61 + a65 = 126


a21  + a105 = 126
a25  + a101 = 126


Space Diagonals:
a32 + a94 = 126
a34 + a92 = 126
a42 + a84 = 126
a44 + a82 = 126

Planes 12/14:

a26 + a100 = 126
a27 + a99  = 126
a29 + a97  = 126
a30 + a96  = 126
a31 + a95  = 126
a35 + a91  = 126
a41 + a85  = 126
a45 + a81  = 126
a46 + a80  = 126
a47 + a79  = 126
a49 + a77  = 126
a50 + a76  = 126


Plane 13:
a57 + a69 = 126
a58 + a68 = 126
a59 + a67 = 126
a62 + a64 = 126

Vertical Planes :
Plane 22:
a2   + a122 = 126
a22  + a102 = 126

Plane 23:
a3   + a123 = 126
a23  + a103 = 126
a78  + a48  = 126
a98  + a28  = 126

Plane 24:
a4   + a124 = 126
a24  + a104 = 126


Plane 23:
a33 + a93 = 126
a43 + a83 = 126


Plane 32:
a6   + a110 = 126
a10  + a106 = 126

Plane 33:
a11  + a115 = 126
a15  + a111 = 126
a36  + a90  = 126
a40  + a86  = 126

Plane 34:
a16  + a120 = 126
a20  + a116 = 126


Plane 33:
a37 + a89 = 126
a39 + a87 = 126

which results, after deduction, in following set of linear equations describing the Perfect Magic Cube of the 5th order as found by Walter Trump: 

a(121) =  315 - a(122) - a(123) - a(124) - a(125) 
a(116) =  315 - a(117) - a(118) - a(119) - a(120) 
a(113) = 1575 - 2 * a(114) - 2 * a(115) - 2 * a(118) - 4 * a(119) - 4 * a(120) - 2 * a(123) - 4 * a(124) - 4 * a(125) 
a(111) =  315 - a(112) - a(113) - a(114) - a(115) 
a(109) =        a(110) - a(113) + a(115) - a(117) + a(120) - a(121) + a(125) 
a(108) =  315 - 4 * a(110) + a(112) + 3 * a(113) + a(114) - 4 * a(116) - a(118) 
a(107) =        a(109) - a(112) + a(114) - a(117) + a(119) - 2 * a(122) + 2 * a(124) 
a(106) =  315 - a(107) - a(108) - a(109) - a(110) 
a(105) =  315 - a(109) - a(113) - a(117) - a(121) 
a(104) =  315 - a(109) - a(114) - a(119) - a(124) 
a(103) =  315 - a(108) - a(113) - a(118) - a(123) 
a(102) =  315 - a(107) - a(112) - a(117) - a(122) 
a(101) =  315 - a(102) - a(103) - a(104) - a(105) 
a( 96) =  315 - a( 97) - a( 98) - a( 99) - a(100) 
a( 93) = 1050 - 2 * {a( 94) + a( 95) + a(125)} - a(123) + {-2 * a(98) - 4 * a(99) - 4 * a(100) - a(112) + a(114) +
              - 4 *  a(117) - 2 * a(118) - 4 * a(120) - 5 * a(122) - a(124)}/3 
a( 92) =  315 - a( 93) - a( 94) - 2 * a(95) + 2 * {a(96) - a(100) + a(116) - a(120)}/3 + a(121) - a(125) 
a( 91) =  315 - a( 92) - a( 93) - a( 94) - a(95) 
a( 89) =        a( 93) - a(115) + a(123) + { -2 * a(90) + 2 * a(95) + 2 * a(98) - 2 * a(99) + a(108) - a(110) - a(112) +
              - a(114) + a(118) - a(120) + a(122) + a(124)}/3 
a( 88) =      - 2 * a(89) - 2 * a(90) + a(93) + 2 * a(94) + 2 * a(95) + a(111) - a(115) - a(121) + a(125) 
a( 87) =        a( 89) + a( 92) - a( 94) 
a( 86) =  315 - a( 87) - a( 88) - a( 89) - a( 90) 
a( 85) =-2898 - a( 90) - a( 97) - a( 98) + { 18 * a(94) + 7 * a(95) + 7 * a(99) - 2 * a(100) + 10 * a(110) + 12 * a(114) + 
         + 18 * a(115) + 12 * a(118) + 24 * a(119) + 34 * a(120) + 10 * a(122) + 18 * a(123) + 34 * a(124) + 48 * a(125)}/5 
a( 84) =        a( 85) - a( 88) + a( 90) - a( 92) + a(95) - a(96) + a(100) 
a( 83) =  945 - a( 87) - a( 94) - 1.5 * {  a( 85) + a(90) + a(95) + a(97) + a(98) + a( 99) + 2 * a(100)} 
a( 82) = {315 - a( 83) - a( 84) - a( 85) + a( 86) - a(88) + a(91) - a(94) + a(96) - a(100)}/2 
a( 81) =  315 - a( 82) - a( 83) - a( 84) - a( 85) 
a( 80) =  315 - a( 84) - a( 88) - a( 92) - a( 96) 
a( 79) =  315 - a( 84) - a( 89) - a( 94) - a( 99) 
a( 78) =  315 - a( 83) - a( 88) - a( 93) - a( 98) 
a( 77) =  315 - a( 82) - a( 87) - a( 92) - a( 97) 
a( 76) =  315 - a( 77) - a( 78) - a( 79) - a( 80) 
a( 75) =   63 + a( 76) - a(100) + a(101) - a(125) 
a( 74) =   63 + a( 77) - a( 99) + a(102) - a(122) 
a( 73) =  378 + a( 79) - a( 99) - a(110) - a(115) - a(120) - 2 * a(125) 
a( 72) =        a( 74) + a(112) - a(114) - 2 * {a(97) - a(99) - a(117) + a(119) - a(122) + a(124)} 
a( 71) =  315 - a( 72) - a( 73) - a( 74) - a( 75) 
a( 70) =   63 + a( 81) - a( 95) + a(116) - a(120) 
a( 69) =   63 + a( 82) - a( 94) 
a( 68) = - 63 + a( 69) + a( 70) - a( 81) - a( 92) + a(94) + a(95) - a(116) + a(120) 
a( 67) =   63 + a( 84) - a( 92) 
a( 66) =  315 - a( 67) - a( 68) - a( 69) - a( 70) 
a( 65) =   63 + a( 91) - a( 95) + a(121) - a(125) 
a( 64) =   63 + a( 92) - a( 94)

a( 63) =  63
a( 62) = 126 - a(64)
a( 61) = 126 - a(65)
a( 60) = 126 - a(66)
a( 59) = 126 - a(67)
a( 58) = 126 - a(68)
a( 57) = 126 - a(69)
a( 56) = 126 - a(70)
a( 55) = 126 - a(71)
a( 54) = 126 - a(72)
a( 53) = 126 - a(73)
a( 52) = 126 - a(74)
a( 51) = 126 - a(75)
a( 50) = 126 - a(76)
a( 49) = 126 - a(77)

a( 48) = 126 - a(78)
a( 47) = 126 - a(79)
a( 46) = 126 - a(80)
a( 45) = 126 - a(81)
a( 44) = 126 - a(82)
a( 43) = 126 - a(83)
a( 42) = 126 - a(84)
a( 41) = 126 - a(85)
a( 40) = 126 - a(86)
a( 39) = 126 - a(87)
a( 38) = 126 - a(88)
a( 37) = 126 - a(89)
a( 36) = 126 - a(90)
a( 35) = 126 - a(91)
a( 34) = 126 - a(92)
a( 33) = 126 - a(93)

a(32) = 126 - a( 94)
a(31) = 126 - a( 95)
a(30) = 126 - a( 96)
a(29) = 126 - a( 97)
a(28) = 126 - a( 98)
a(27) = 126 - a( 99)
a(26) = 126 - a(100)
a(25) = 126 - a(101)
a(24) = 126 - a(104)
a(23) = 126 - a(103)
a(22) = 126 - a(102)
a(21) = 126 - a(105)
a(20) = 126 - a(116)
a(19) = 126 - a(119)
a(18) = 126 - a(118)
a(17) = 126 - a(117)

a(16) = 126 - a(120)
a(15) = 126 - a(111)
a(14) = 126 - a(114)
a(13) = 126 - a(113)
a(12) = 126 - a(112)
a(11) = 126 - a(115)
a(10) = 126 - a(106)
a( 9) = 126 - a(109)
a( 8) = 126 - a(108)
a( 7) = 126 - a(107)
a( 6) = 126 - a(110)
a( 5) = 126 - a(121)
a( 4) = 126 - a(124)
a( 3) = 126 - a(123)
a( 2) = 126 - a(122)
a( 1) = 126 - a(125)

The linear equations shown above, are ready to be solved, for the magic constant 315.

The solutions can be obtained by guessing:

   a( 90), a( 94), a( 95), a( 97) ... a(100)
   a(110), a(112), a(114), a(115),    a(117) ... a(120), a(122) ... a(125)

and filling out these guesses in the abovementioned equations.

For distinct integers also following relations should be applied:

0 < a(i) =< 125       for i =   1 ...  89,  91 ... 93,  96
                      and i = 101 ... 109, 111,   113, 116, 121
Int(a(i)) = a(i)      for i = 82, 83, 85, 89, 92, 93
a(i) ≠ a(j)           for i ≠ j

which can be incorporated in a guessing routine, which might be used to find other 5th order Perfect Magic Cubes.

However the total number of independent variables (19) is to large to find more results within a reasonable time.

4.2b Additional Solutions, Perfect Magic Cubes

Although the total number of independent variables is too large to find much more results within a reasonable time, an appropriate guessing routine (MgcCube5a2) produced - based on the top squares of eight earlier published Perfect Magic Cubes - eight additional Perfect Magic Cubes (ca. 650 seconds per known top square).

Subject Perfect Magic Cubes - shown in Attachment 4.2.1, page 1 - can also be obtained by a transformation illustrated and described in Attachment 4.2.2.

In addition to this another 16 (unique) Perfect Magic Cubes could be generated based on a transformation of subject top squares (exchanged border lines), as shown in Attachment 4.2.1, page 2.

4.2c More Transformations, Perfect Magic Cubes

Comparable with 5th order Magic Squares (ref. 'Magic Squares' Section 3.5), Perfect Magic Cubes of order 5 might be subject to following transformations:

  • A permutation can be applied to the planes 1, 2 provided that the same permutation is applied to the planes 5, 4;

  • Any plane n can be interchanged with plane (6 - n), as well as the combination of these two permutations, resulting in 4 transformations (2 unique);

  • Combination of abovementioned transformations will result in 4 unique solutions, which are shown in Attachment 4.2.3.

Note: Secondary properties, like the applied symmetry, are not invariant to the transformations described above.

Based on these four transformations and the 48 cubes which can be found by means of rotation and/or reflection (ref. Attachment 4.1) any 5th order (Perfect) Magic Cube corresponds with a Class of 4 * 48 = 192 (Perfect) Magic Cubes.

Vorige Pagina Volgende Pagina Index About the Author