Office Applications and Entertainment, Magic Cubes | ||
|
|
Index | About the Author |
|
Plane 11 (Top)
|
||||||||||||||||||||||||||
|
Plane 12
|
|||||||||||||||||||||||||||
|
Plane 13
|
|||||||||||||||||||||||||||
|
Plane 14
|
|||||||||||||||||||||||||||
|
Plane 15
|
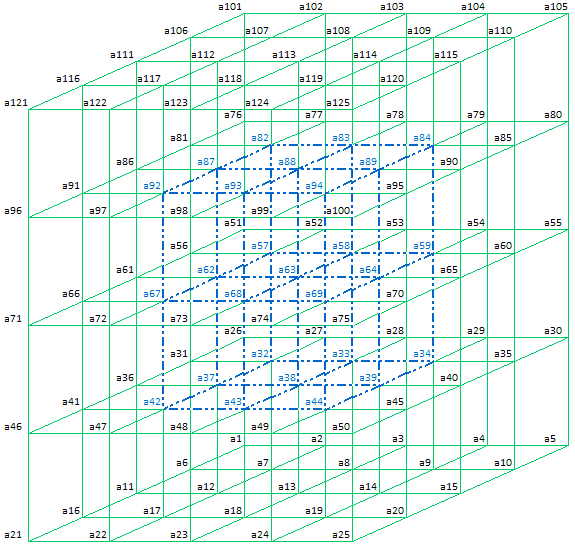
The Embedded Simple Magic Cube can be described by following linear equations (Section 2.2):
Rows:
Columns:
Pillars:
Space Diagonals:
a82 + a83 + a84 = 189
a87 + a88 + a89 = 189
a92 + a93 + a94 = 189
a57 + a58 + a59 = 189
a62 + a63 + a64 = 189
a67 + a68 + a69 = 189
a32 + a33 + a34 = 189
a37 + a38 + a39 = 189
a42 + a43 + a44 = 189
a82 + a87 + a92 = 189
a83 + a88 + a93 = 189
a84 + a89 + a94 = 189
a57 + a62 + a67 = 189
a58 + a63 + a68 = 189
a59 + a64 + a69 = 189
a32 + a37 + a42 = 189
a33 + a38 + a43 = 189
a34 + a39 + a44 = 189
a82 + a57 + a32 = 189
a87 + a62 + a37 = 189
a92 + a67 + a42 = 189
a83 + a58 + a33 = 189
a88 + a63 + a38 = 189
a93 + a68 + a43 = 189
a84 + a59 + a34 = 189
a89 + a64 + a39 = 189
a94 + a69 + a44 = 189
a42 + a63 + a84 = 189
a44 + a63 + a82 = 189
a34 + a63 + a92 = 189
a32 + a63 + a94 = 189
|
As mentioned in Section 4.1 it can be proven for 5th order Magic Cubes that Bordered Perfect Magic Cubes donít exist.
However if for a Magic Cube of order 5, the equations of the magic border squares are combined with the required symmetry conditions:
this will result, after deduction, in following set of linear equations, describing the border of a Bordered Magic Cube of the 5th order:
a121 = 315 - a122 - a123 - a124 - a125
a116 = 315 - a117 - a118 - a119 - a120
a111 = 315 - a112 - a113 - a114 - a115
a109 = a110 - a113 + a115 - a117 + a120 - a121 + a125
a107 = (315 - a108 - a109 - a110 + a111 - a113 + a116 - a119 + a121 - a125)/2
a106 = 315 - a107 - a108 - a109 - a110
a105 = 315 - a109 - a113 - a117 - a121
a104 = 315 - a109 - a114 - a119 - a124
a103 = 315 - a108 - a113 - a118 - a123
a102 = 315 - a107 - a112 - a117 - a122
a101 = 315 - a102 - a103 - a104 - a105
a96 = 315 - a97 - a98 - a99 - a100
a85 = 189 - a90 - a95 + a96 - a100
a73 = -315 + a74 - a97 + a99 + a101 + a110 - a113 + a114 + a115 - a117 + a119 + a120 - 2 * a121 + 2 * a124 + a125
a72 = 630 + 2 * a73 - a74 - a112 + 2 * a113 - a114 - 4 * a122 - 2 * a123 - 4 * a124
a71 = 315 - a72 - a73 - a74 - a75
a70 =(8316-3*a74-2*a75-3*a90-6*a95-3*a98-6*a99-6*a100-2*a108-8*a110-2*a112+2*a113-5*a114-10*a115- 5*a118- 6*a119 +
-14*a120-8*a122-10*a123-14*a124-18*a125)/3
a65 = -378 - a66 + a90 + 2 * a95 - a96 + a100 + a101 + a110 + a115 - a116 + 2 * a120 + a125
a60 = 126 + a65 + a90 +2 * a95 - a96 + a100 - a107 - a108 - 3*a110 + a113 - a115 + a117 - a120
a50 = 189 - a75 - a100 +a101 - a125
a49 = 819 - a74 - a99 - a110 + a113 - a114 - a115 + a117 - a119 - a120 - a122 - a123 - 3*a124 - 2*a125
a48 = 504 - a73 - a98 - a108 - a113 - a118 - 2 * a123
a47 = 504 - a73 - a99 - a110 - a115 - a120 - 2 * a125
a46 = 315 - a47 - a48 - a49 - a50
a45 = -945 + a56 + 2*a90 + 3*a95 + 2*a97 + 2*a98 + 2*a99 + 4*a100 - a111 + a115 - a116 + a120 - 2*a121 + 2*a125
a40 = 630 - a41 - a49 - a73 + a85 - a90 - a97 - a110 + a111 - 2 * a115 - a120 - a121 - a125
a35 = 126 - a36 + a90 - a95 - a111 + a115 + a121 - a125
The linear equations shown above, can be incorporated in a guessing routine, which might be used to find other suitable borders.
With the border variables constant, a simplified guessing routine (MgcCube5b1) produced 192 Bordered Magic Cubes within
40 seconds, which are shown in Attachment 4.3.1
and Attachment 4.3.2.
4.3b Alternative Solution Bordered Magic Cubes
Alternatively Bordered Magic Cubes can be constructed based on Complementary Anti Symmetric Magic Squares of order 5.
with Pr5 = 2 * s1 / 5 the pair sum for the corresponding Magic Sum s1.
the defining equations of the Magic Back Square can be written as: a( 6) = s1 - a( 7) - a( 8) - a( 9) - a(10) a( 7) = s1 - a(13) - a(19) - a( 1) - a(25) a( 8) = s1 - a(13) - a(18) - a( 3) - a(23) a( 9) = s1 - a(14) - a(19) - a( 4) - a(24) a(10) = s1 - a(15) - a(20) - a( 5) - a(25) a(11) = s1 - a( 6) - a(16) - a( 1) - a(21) a(12) = s1 - a( 7) - a(17) - a( 2) - a(22) a(13) = a(14) - a(17) + a(19) + a( 4) - a(5) - a(21) + a(24) a(16) = s1 - a(17) - a(18) - a(19) - a(20)
with a(i) independent for i = 14, 15††and i = 17 ... 20;
the defining equations of the Left Magic Square can be written as:
a( 7) = s1 - a(13) - a(19) - a( 1) - a(25)
a( 8) = s1 - a(13) - a(18) - a( 3) - a(23)
a( 9) = s1 - a(14) - a(19) - a( 4) - a(24)
a(12) = s1 - a(13) - a(14) - a(11) - a(15)
a(13) = a(14) - a(17) + a(19) + a(4) - a( 5) - a(21) + a(24)
a(14) = (-3*a(18) -6*a(19) - a(11) - a(15)- 3*a(16) - 3*a(20) + a( 1) +
+ 3*a( 2) + 2*a( 3) +4*a( 5) + 4*a(21) + 3*a(22) + 2*a(23) + a(25))/3
a(17) = s1 - a(18) - a(19) - a(16) - a(20)
with a(i) independent for i = 18 and 19;
Attachment 4.3.6 shows, for the Anti Symmetric Magic Squares enclosed in Attachment 4.3.5, the first occurring Bordered Magic Cube with 6 Magic Surface Planes.
|
|
|
Index | About the Author |