|
7.5 Concentric and Eccentric Magic Squares
7.5.1 Concentric Magic Squares (1)
In general an odd Concentric Magic Square consists of a centre of one cell around which borders can be constructed again and again.
A 7th order Concentric Magic Square consists of an Embedded Magic Square of the 5th order with an Embedded Magic Square of the 3th order.
| a(1) |
a(2) |
a(3) |
a(4) |
a(5) |
a(6) |
a(7) |
| a(8) |
a(9) |
a(10) |
a(11) |
a(12) |
a(13) |
a(14) |
| a(15) |
a(16) |
a(17) |
a(18) |
a(19) |
a(20) |
a(21) |
| a(22) |
a(23) |
a(24) |
a(25) |
a(26) |
a(27) |
a(28) |
| a(29) |
a(30) |
a(31) |
a(32) |
a(33) |
a(34) |
a(35) |
| a(36) |
a(37) |
a(38) |
a(39) |
a(40) |
a(41) |
a(42) |
| a(43) |
a(44) |
a(45) |
a(46) |
a(47) |
a(48) |
a(49) |
The Embedded Magic Square can be described by following linear equations:
a(37) = 125 - a(38) - a(39) - a(40) - a(41)
a(31) = 75 - a(32) - a(33)
a(30) = 50 - a(34)
a(26) = 100 - a(32) - 2 * a(33)
a(25) = 25
a(24) = 50 - a(26)
a(23) = 50 - a(27)
a(20) = 75 - a(27) - a(34) + a(37) - a(41)
a(19) = 50 - a(31)
a(18) = 50 - a(32)
a(17) = 50 - a(33)
a(16) = 50 - a(20)
a(13) = 50 - a(37)
a(12) = 50 - a(40)
a(11) = 50 - a(39)
a(10) = 50 - a(38)
a( 9) = 50 - a(41)
which can be completed with the equations describing the outer border, which results in following linear equations:
a(43) = 175 - a(44) - a(45) - a(46) - a(47) - a(48) - a(49)
a(37) = 125 - a(38) - a(39) - a(40) - a(41)
a(36) = 50 - a(42)
a(31) = 75 - a(32) - a(33)
a(30) = 50 - a(34)
a(29) = 50 - a(35)
a(26) = 100 - a(32) - 2 * a(33)
a(25) = 25
a(24) = 50 - a(26)
a(23) = 50 - a(27)
a(22) = 50 - a(28)
a(20) = 75 - a(27) - a(34) + a(37) - a(41)
a(19) = 50 - a(31)
a(18) = 50 - a(32)
a(17) = 50 - a(33)
a(16) = 50 - a(20)
a(15) = 50 - a(21)
a(14) = -75 + a(15) + a(22) + a(29) + a(36) + a(43) - a(49)
a(13) = 50 - a(37)
a(12) = 50 - a(40)
a(11) = 50 - a(39)
a(10) = 50 - a(38)
a( 9) = 50 - a(41)
a( 8) = 50 - a(14)
a( 7) = 50 - a(43)
a( 6) = 50 - a(48)
a( 5) = 50 - a(47)
a( 4) = 50 - a(46)
a( 3) = 50 - a(45)
a( 2) = 50 - a(44)
a( 1) = 50 - a(49)
Note: The Embedded Magic Square is based on the consecutive integers 13, 14, ... 37.
With the exterior border variables constant, an optimized guessing routine (MgcSqr7d), will produce the 23040 possible Magic Squares, of which 2880 (based on one interior Magic Square of the 3th oder) are shown in Attachment 7.5.1.
With the Embedded Magic Squares and the variables a(49), a(48) and a(47) constant, the same optimized guessing routine, produced 7920 Magic Squares within 16 minutes, which are shown in Attachment 7.5.2.
With only the Embedded Magic Squares constant, the same optimized guessing routine, counted 21312000
Concentric Magic Squares within about 10 hours.
The total number of Concentric Magic Squares of the 7th order will be 23040 * 21312000 = 4.91 1011.
It should be noted that even more Concentric Magic Squares can be generated with routine MgcSqr7d, when the base for the Embedded Magic Squares is not limited to the consecutive integers 13, 14, ... 37.
7.5.2 Concentric Magic Squares (2)
Alternatively the border of a 7th order Concentric Magic Square can be described by following equations:
a(44) = 175 - a(43) - a(45) - a(46) - a(47) - a(48) - a(49)
a(14) = 175 - a( 7) - a(21) - a(28) - a(35) - a(42) - a(49)
a( 7) = 50 - a(43)
a( 8) = 50 - a(14)
a( 6) = 50 - a(48)
a(15) = 50 - a(21)
a( 5) = 50 - a(47)
a(22) = 50 - a(28)
a( 4) = 50 - a(46)
a(29) = 50 - a(35)
a( 3) = 50 - a(45)
a(36) = 50 - a(42)
a( 2) = 50 - a(44)
a( 1) = 50 - a(49)
The resulting solutions will be unique when following conditions are added to the equations listed above:
a( 7) < a(43) < a(49)
prevent rotation and reflection
a(44) < a(45) < a(46) < a(47) < a(48) prevent permutation of non corner variables
a(14) < a(21) < a(28) < a(35) < a(42)
An optimized guessing routine (MgcSqr7d2) produced,
based on the integers 1 ... 12 and 38 ... 49, 185 suitable unique borders within 12,3 seconds,
which are shown in Attachment Attachment 7.5.4.
Consequently, the total number of borders will be 185 * 8 * (5!)2 = 21312000 as found in Section 7.5.1 above.
7.5.3 Eccentric Magic Squares (1)
An Eccentric Magic Square can be defined as a Magic Corner Square of order n, supplemented with two or more (i) rows and columns to a Magic Square of order (n + i).
A 7th order Eccentric Magic Square consists of one Magic Corner Square of the 5th order, supplemented with two rows and two columns.
| a(1) |
a(2) |
a(3) |
a(4) |
a(5) |
a(6) |
a(7) |
| a(8) |
a(9) |
a(10) |
a(11) |
a(12) |
a(13) |
a(14) |
| a(15) |
a(16) |
a(17) |
a(18) |
a(19) |
a(20) |
a(21) |
| a(22) |
a(23) |
a(24) |
a(25) |
a(26) |
a(27) |
a(28) |
| a(29) |
a(30) |
a(31) |
a(32) |
a(33) |
a(34) |
a(35) |
| a(36) |
a(37) |
a(38) |
a(39) |
a(40) |
a(41) |
a(42) |
| a(43) |
a(44) |
a(45) |
a(46) |
a(47) |
a(48) |
a(49) |
If the 5th order Magic Corner Square is an Eccentric Magic Square itself, it can be described by following linear equations:
a(47) = 75 - a(48) -a(49)
a(45) = 50 - a(46)
a(42) = 100 - a(48) - 2 * a(49)
a(41) = 25
a(40) = 50 - a(42)
a(38) = 50 - a(39)
a(35) = 50 - a(47)
a(34) = 50 - a(48)
a(33) = 50 - a(49)
a(31) = 50 - a(32)
a(27) = 75 + a(28) - a(33) - a(39) - a(45)
a(25) = 50 - 0.5 * (a(26) + a(27) + a(28) + a(32) - a(38) - a(45))
a(24) = 125 - a(25) - a(26) - a(27) - a(28)
a(21) = 50 - a(28)
a(20) = 50 - a(27)
a(19) = 50 - a(26)
a(18) = 50 - a(24)
a(17) = 50 - a(25)
which can be combined with the equations describing a Magic Square of the 7th order (Section 7.1), and result in following linear equations:
a(47) = 75 - a(48) -a(49)
a(45) = 50 - a(46)
a(43) = 50 - a(44)
a(42) = 100 - a(48) - 2 * a(49)
a(41) = 25
a(40) = 50 - a(42)
a(38) = 50 - a(39)
a(36) = 50 - a(37)
a(35) = 50 - a(47)
a(34) = 50 - a(48)
a(33) = 50 - a(49)
a(31) = 50 - a(32)
a(29) = 50 - a(30)
a(27) = 75 + a(28) - a(33) - a(39) - a(45)
a(25) = 50 - 0.5 * (a(26) + a(27) + a(28) + a(32) - a(38) - a(45))
a(24) = 125 - a(25) - a(26) - a(27) - a(28)
a(22) = 50 - a(23)
a(21) = 50 - a(28)
a(20) = 50 - a(27)
a(19) = 50 - a(26)
a(18) = 50 - a(24)
a(17) = 50 - a(25)
a(15) = 50 - a(16)
a(13) = 125 + a(14) - a(19) - a(25) - a(31) - a(37) - a(43)
a( 9) = 150 - 0.5 * (a(10) + a(11) + a(12) + a(13) + a(14) + a(16) + a(23) + a(30) + a(37) + a(44))
a( 8) = -125 + a( 9) + a(16) + a(23) + a(30) + a(37) + a(44)
a( 7) = 50 - a(14)
a( 6) = 50 - a(13)
a( 5) = 50 - a(12)
a( 4) = 50 - a(11)
a( 3) = 50 - a(10)
a( 2) = 50 - a( 8)
a( 1) = 50 - a( 9)
Note: The Magic Corner Square is based on the consecutive integers 13, 14, ... 37.
Rather than starting with the equations of the Magic Corner Square, the equations of the supplementary rows and columns can be used as a starting point for the generation of Eccentric Magic Squares.
| a(1) |
a(2) |
a(3) |
a(4) |
a(5) |
a(6) |
a(7) |
| a(8) |
a(9) |
a(10) |
a(11) |
a(12) |
a(13) |
a(14) |
| a(15) |
a(16) |
a(17) |
a(18) |
a(19) |
a(20) |
a(21) |
| a(22) |
a(23) |
a(24) |
a(25) |
a(26) |
a(27) |
a(28) |
| a(29) |
a(30) |
a(31) |
a(32) |
a(33) |
a(34) |
a(35) |
| a(36) |
a(37) |
a(38) |
a(39) |
a(40) |
a(41) |
a(42) |
| a(43) |
a(44) |
a(45) |
a(46) |
a(47) |
a(48) |
a(49) |
The supplementary rows and columns can be described by following linear equations:
a( 1) + a( 2) + a( 3) + a( 4) + a( 5) + a( 6) + a( 7) = 175
a( 8) + a( 9) + a(10) + a(11) + a(12) + a(13) + a(14) = 175
a( 1) + a( 8) + a(15) + a(22) + a(29) + a(36) + a(43) = 175
a( 2) + a( 9) + a(16) + a(23) + a(30) + a(37) + a(44) = 175
a( 7) + a(13) + a(19) + a(25) + a(31) + a(37) + a(43) = 175
a( 1) + a( 9) = 50
a( 3) + a(10) = 50
a( 4) + a(11) = 50
a( 5) + a(12) = 50
a( 6) + a(13) = 50
a( 7) + a(14) = 50
a(15) + a(16) = 50
a(22) + a(23) = 50
a(29) + a(30) = 50
a(36) + a(37) = 50
a(43) + a(44) = 50
Which can be reduced, by means of row and column manipulations, to:
a(43) = 50 - a(44)
a(36) = 50 - a(37)
a(29) = 50 - a(30)
a(22) = 50 - a(23)
a(15) = 50 - a(16)
a(13) = 125 + a(14) - a(19) - a(25) - a(31) - a(37) - a(43)
a( 9) = 150 - 0.5 * (a(10) + a(11) + a(12) + a(13) + a(14) + a(16) + a(23) + a(30) + a(37) + a(44))
a( 8) = -125 + a( 9) + a(16) + a(23) + a(30) + a(37) + a(44)
a( 7) = 50 - a(14)
a( 6) = 50 - a(13)
a( 5) = 50 - a(12)
a( 4) = 50 - a(11)
a( 3) = 50 - a(10)
a( 2) = 50 - a( 8)
a( 1) = 50 - a( 9)
It is even more obvious that the number of Eccentric Magic Squares is determined by the sum (s2) of the values of the key variables
a(31), a(25) and a(19).
An optimized guessing routine (MgcSqr7e) produced,
based on the (Eccentric) Magic Corner Square of the 5th order as shown in the Spreadsheet Solution below and a(44) = 1,
864 Eccentric Magic Squares within 12,5 minutes, which are shown in Attachment 7.5.3.
The same routine produced, based on one Pan Magic Square of the fifth order, a(44) = 1 and a(37) = 2,
3888 Eccentric Magic Squares within 8,6 minutes, which are shown in Attachment 7.5.4.
7.5.4 Eccentric Magic Squares (2)
Alternatively the supplementary rows and columns - further referred to as 'border' -
of a 7th order Eccentric Magic Square can be described by following equations:
a( 7) = 175 - a(13) - s2 - a(37) - a(43)
a(16) = 175 - a(44) - a(37) - a(30) - a(23) - a(9) - a(2)
a(10) = 175 - a(14) - a(13) - a(12) - a(11) - a(9) - a(8)
a(14) = 50 - a( 7)
a(15) = 50 - a(16)
a( 6) = 50 - a(13)
a(22) = 50 - a(28)
a( 5) = 50 - a(12)
a(29) = 50 - a(30)
a( 4) = 50 - a(11)
a(36) = 50 - a(37)
a( 3) = 50 - a(10)
a(44) = 50 - a(43)
a( 2) = 50 - a( 8)
a( 1) = 50 - a( 9)
The resulting solutions will be unique when following conditions are added to the equations listed above:
a( 2) < a( 8)
prevent mirroring around diagonal a(1) ... a(49)
a(16) < a(23) < a(30) prevent permutation of subject variables
a(10) < a(11) < a(12)
An optimized guessing routine (MgcSqr7e2) produced,
based on the integers 1 ... 12 and 38 ... 49, while varying s2, 126504 unique borders.
The breakdown of these borders as a function of s2 is shown in the graph below.
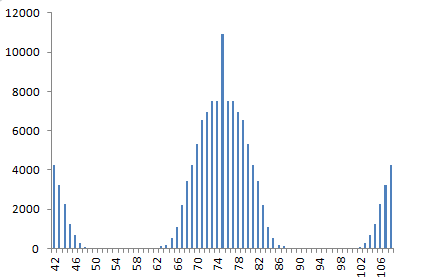
The actual number of borders Nb can be obtained by multiplication with 2 * 62 (= 72).
It should be noted that even more Eccentric Magic Squares can be generated with routine MgcSqr7e, when the base for the Magic Corner Squares is not limited to the consecutive integers 13, 14, ... 37.
7.5.5 Spreadsheet Solutions
The linear equations deducted in Section 7.5.1 and 7.5.3 above, have been applied in following Excel Spread Sheets:
Only the red figures have to be guessed to construct one of the applicable 7th order Magic Squares (wrong solutions are obvious).
| 