Office Applications and Entertainment, Magic Squares

8.4   Franklin Squares, Bent Diagonals

8.4.1 Introduction

Following well known Magic Square was constructed by Benjamin Franklin:

52	61	4	13	20	29	36	45
14	3	62	51	46	35	30	19
53	60	5	12	21	28	37	44
11	6	59	54	43	38	27	22
55	58	7	10	23	26	39	42
9	8	57	56	41	40	25	24
50	63	2	15	18	31	34	47
16	1	64	49	48	33	32	17

The square has been constructed based on following properties:

1. The numbers of every row and column sum to the Magic Constant;
2. In every half-row and half-column the numbers sum to half the Magic Constant;
3. The numbers of the main bent diagonals and all the bent diagonals parallel to it sum to the Magic Constant;
4. The four corner numbers together with the four middle numbers sum to the Magic Constant;
5. The numbers of every 2 × 2 sub square sum to half the Magic Constant.

The first property is, of course, included in the second. Further it is worth noticing that the fourth property, listed by Benjamin Franklin becomes redundant, with the assumption of the fifth property.

The concept of main and parallel bent diagonals is illustrated in Attachment 8.4.1.

8.4.2 Analysis

The properties described in section 8.4.1 above result in following linear equations for a Franklin Square of the 8^th order.

Every half-row and half-column sums to half the Magic Constant:

The numbers of the main bent diagonals and all the bent diagonals parallel to it sum to the Magic Constant:

a( 1) + a(10) + a(19) + a(28) + a(36) + a(43) + a(50) + a(57) = s1
a( 2) + a(11) + a(20) + a(29) + a(37) + a(44) + a(51) + a(58) = s1
a( 3) + a(12) + a(21) + a(30) + a(38) + a(45) + a(52) + a(59) = s1
a( 4) + a(13) + a(22) + a(31) + a(39) + a(46) + a(53) + a(60) = s1
a( 5) + a(14) + a(23) + a(32) + a(40) + a(47) + a(54) + a(61) = s1
a( 6) + a(15) + a(24) + a(25) + a(33) + a(48) + a(55) + a(62) = s1
a( 7) + a(16) + a(17) + a(26) + a(34) + a(41) + a(56) + a(63) = s1
a( 8) + a( 9) + a(18) + a(27) + a(35) + a(42) + a(49) + a(64) = s1

a( 8) + a(15) + a(22) + a(29) + a(37) + a(46) + a(55) + a(64) = s1
a( 7) + a(14) + a(21) + a(28) + a(36) + a(45) + a(54) + a(63) = s1
a( 6) + a(13) + a(20) + a(27) + a(35) + a(44) + a(53) + a(62) = s1
a( 5) + a(12) + a(19) + a(26) + a(34) + a(43) + a(52) + a(61) = s1
a( 4) + a(11) + a(18) + a(25) + a(33) + a(42) + a(51) + a(60) = s1
a( 3) + a(10) + a(17) + a(32) + a(40) + a(41) + a(50) + a(59) = s1
a( 2) + a( 9) + a(24) + a(31) + a(39) + a(48) + a(49) + a(58) = s1
a( 1) + a(16) + a(23) + a(30) + a(38) + a(47) + a(56) + a(57) = s1

a( 1) + a(10) + a(19) + a(28) + a(29) + a(22) + a(15) + a( 8) = s1
a( 9) + a(18) + a(27) + a(36) + a(37) + a(30) + a(23) + a(16) = s1
a(17) + a(26) + a(35) + a(44) + a(45) + a(38) + a(31) + a(24) = s1
a(25) + a(34) + a(43) + a(52) + a(53) + a(46) + a(39) + a(32) = s1
a(33) + a(42) + a(51) + a(60) + a(61) + a(54) + a(47) + a(40) = s1
a(41) + a(50) + a(59) + a( 4) + a( 5) + a(62) + a(55) + a(48) = s1
a(49) + a(58) + a( 3) + a(12) + a(13) + a( 6) + a(63) + a(56) = s1
a(57) + a( 2) + a(11) + a(20) + a(21) + a(14) + a( 7) + a(64) = s1

a(57) + a(50) + a(43) + a(36) + a(37) + a(46) + a(55) + a(64) = s1
a(49) + a(42) + a(35) + a(28) + a(29) + a(38) + a(47) + a(56) = s1
a(41) + a(34) + a(27) + a(20) + a(21) + a(30) + a(39) + a(48) = s1
a(33) + a(26) + a(19) + a(12) + a(13) + a(22) + a(31) + a(40) = s1
a(25) + a(18) + a(11) + a( 4) + a( 5) + a(14) + a(23) + a(32) = s1
a(17) + a(10) + a( 3) + a(60) + a(61) + a( 6) + a(15) + a(24) = s1
a( 9) + a( 2) + a(59) + a(52) + a(53) + a(62) + a( 7) + a(16) = s1
a( 1) + a(58) + a(51) + a(44) + a(45) + a(54) + a(63) + a( 8) = s1

Every 2 × 2 sub square sums to half the Magic Constant:

a(i) + a(i+1) + a(i+ 8) + a(i+ 9) = s1/2 with 1 =< i < 56 and i ≠ 8*n for n = 1, 2 ... 7

a(i) + a(i+1) + a(i+ 8) + a(i- 7) = s1/2 with i = 8*n for n = 1, 2 ... 7

a(i) + a(i+1) + a(i+56) + a(i+57) = s1/2 with i = 1, 2 ... 7

a(1) + a(8)   + a(57)   + a(64)   = s1/2

The resulting number of equations can be written in the matrix representation as:

           →   →
     A_F1 * a = s

which can be reduced, by means of row and column manipulations, and results in following set of linear equations:

a(61) =  0.5 * s1 - a(62) - a(63) - a(64)
a(58) =           - a(60) + a(62) + a(64)
a(57) =  0.5 * s1 - a(59) - a(62) - a(64)
a(55) =  0.5 * s1 - a(56) - a(63) - a(64)
a(54) =             a(56) - a(62) + a(64)
a(53) =           - a(56) + a(62) + a(63)
a(52) =             a(56) - a(60) + a(64)
a(51) =  0.5 * s1 - a(56) - a(59) - a(64)
a(50) =             a(56) + a(60) - a(62)
a(49) =           - a(56) + a(59) + a(62)
a(47) =           - a(48) + a(63) + a(64)
a(46) =             a(48) + a(62) - a(64)
a(45) =  0.5 * s1 - a(48) - a(62) - a(63)
a(44) =             a(48) + a(60) - a(64)
a(43) =           - a(48) + a(59) + a(64)
a(42) =             a(48) - a(60) + a(62)
a(41) =  0.5 * s1 - a(48) - a(59) - a(62)
a(40) =  0.5 * s1 - a(48) - a(56) - a(64)
a(39) =             a(48) + a(56) - a(63)
a(38) =  0.5 * s1 - a(48) - a(56) - a(62)
a(37) = -0.5 * s1 + a(48) + a(56) + a(62) + a(63) + a(64)
a(36) =  0.5 * s1 - a(48) - a(56) - a(60)
a(35) =             a(48) + a(56) - a(59)
a(34) =  0.5 * s1 - a(48) - a(56) + a(60) - a(62) - a(64)
a(33) = -0.5 * s1 + a(48) + a(56) + a(59) + a(62) + a(64)
a(31) =           - a(32) + a(63) + a(64)
a(30) =             a(32) + a(62) - a(64)
a(29) =  0.5 * s1 - a(32) - a(62) - a(63)
a(28) =             a(32) + a(60) - a(64)
a(27) =           - a(32) + a(59) + a(64)
a(26) =             a(32) - a(60) + a(62)
a(25) =  0.5 * s1 - a(32) - a(59) - a(62)
a(23) =  0.5 * s1 - a(24) - a(63) - a(64)
a(22) =             a(24) - a(62) + a(64)
a(21) =           - a(24) + a(62) + a(63)
a(20) =             a(24) - a(60) + a(64)
a(19) =  0.5 * s1 - a(24) - a(59) - a(64)
a(18) =             a(24) + a(60) - a(62)
a(17) =           - a(24) + a(59) + a(62)
a(16) =           - a(32) + a(48) + a(64)
a(15) =             a(32) - a(48) + a(63)
a(14) =           - a(32) + a(48) + a(62)
a(13) =  0.5 * s1 + a(32) - a(48) - a(62) - a(63) - a(64)
a(12) =           - a(32) + a(48) + a(60)
a(11) =             a(32) - a(48) + a(59)
a(10) =           - a(32) + a(48) - a(60) + a(62) + a(64)
a( 9) =  0.5 * s1 + a(32) - a(48) - a(59) - a(62) - a(64)
a( 8) =  0.5 * s1 - a(24) - a(48) - a(64)
a( 7) =             a(24) + a(48) - a(63)
a( 6) =  0.5 * s1 - a(24) - a(48) - a(62)
a( 5) = -0.5 * s1 + a(24) + a(48) + a(62) + a(63) + a(64)
a( 4) =  0.5 * s1 - a(24) - a(48) - a(60)
a( 3) =             a(24) + a(48) - a(59)
a( 2) =  0.5 * s1 - a(24) - a(48) + a(60) - a(62) - a(64)
a( 1) = -0.5 * s1 + a(24) + a(48) + a(59) + a(62) + a(64)

The solutions can be obtained by guessing a(24), a(32), a(48), a(56), a(59), a(60) and a(62) ... a(64) and filling out these guesses in the abovementioned equations.

For distinct integers also following inequalities should be applied:

0 < a(i) =< 64        for i = 1, 2, ... 23, 25 ... 31, 33 ... 47, 49 ... 55, 57, 58 and 61
a(i) ≠ a(j)           for i ≠ j

With a(64) = 17 and a(63) = 32, an optimized guessing routine (MgcSqr8f), produced 3840 Franklin Squares within 634 seconds, which are shown in Attachment 8.4.2.

8.4.3 Enumeration

The total number of order 8 Franklin Squares (8 * 1.105.920) has been determined in 2006 by Daniel Schindel, Mathes Rempel and Peter Lody (ref. Proceedings of the Royal Society 2006).

A more appropriate routine - in which after the corner points a(64), a(57), a(8) and a(1) the remaining variables are calculated - can be developed.

This sequence together with the properties of an order 8 Franklin Square result, after deduction, in following set of linear equations:

a( 1) =  0.5 * s1 - a( 8) - a(57) - a(64)
a(61) =  0.5 * s1 - a(62) - a(63) - a(64)
a(59) =  0.5 * s1 - a(62) - a(57) - a(64)
a(58) =            -a(60) + a(62) + a(64)
a(55) =  0.5 * s1 - a(56) - a(63) - a(64)
a(54) =             a(56) - a(62) + a(64)
a(53) =           - a(56) + a(62) + a(63)
a(52) =             a(56) - a(60) + a(64)
a(51) =           - a(56) + a(62) + a(57)
a(50) =             a(56) + a(60) - a(62)
a(49) =  0.5 * s1 - a(56) - a(57) - a(64)
a(47) =           - a(48) + a(63) + a(64)
a(46) =             a(48) + a(62) - a(64)
a(45) =  0.5 * s1 - a(48) - a(62) - a(63)
a(44) =             a(48) + a(60) - a(64)
a(43) =  0.5 * s1 - a(48) - a(62) - a(57)
a(42) =             a(48) - a(60) + a(62)
a(41) =           - a(48) + a(57) + a(64)
a(40) =  0.5 * s1 - a(48) - a(56) - a(64)
a(39) =             a(48) + a(56) - a(63)
a(38) =  0.5 * s1 - a(48) - a(56) - a(62)
a(37) = -0.5 * s1 + a(48) + a(56) + a(62) + a(63) + a(64)
a(36) =  0.5 * s1 - a(48) - a(56) - a(60)
a(35) = -0.5 * s1 + a(48) + a(56) + a(62) + a(57) + a(64)
a(34) =  0.5 * s1 - a(48) - a(56) + a(60) - a(62) - a(64)
a(33) =             a(48) + a(56) - a(57)
a(31) =           - a(32) + a(63) + a(64)
a(30) =             a(32) + a(62) - a(64)
a(29) =  0.5 * s1 - a(32) - a(62) - a(63)
a(28) =             a(32) + a(60) - a(64)
a(27) =  0.5 * s1 - a(32) - a(62) - a(57)
a(26) =             a(32) - a(60) + a(62)
a(25) =           - a(32) + a(57) + a(64)
a(24) =  0.5 * s1 - a(48) - a( 8) - a(64)
a(23) =             a(48) - a(63) + a( 8)
a(22) =  0.5 * s1 - a(48) - a(62) - a( 8)
a(21) = -0.5 * s1 + a(48) + a(62) + a(63) + a(8) + a(64)
a(20) =  0.5 * s1 - a(48) - a(60) - a( 8)
a(19) = -0.5 * s1 + a(48) + a(62) + a( 8) + a(57) + a(64)
a(18) =  0.5 * s1 - a(48) + a(60) - a(62) - a(8) - a(64)
a(17) =             a(48) + a( 8) - a(57)
a(16) =           - a(32) + a(48) + a(64)
a(15) =             a(32) - a(48) + a(63)
a(14) =           - a(32) + a(48) + a(62)
a(13) =  0.5 * s1 + a(32) - a(48) - a(62) - a(63) - a(64)
a(12) =           - a(32) + a(48) + a(60)
a(11) =  0.5 * s1 + a(32) - a(48) - a(62) - a(57) - a(64)
a(10) =           - a(32) + a(48) - a(60) + a(62) + a(64)
a( 9) =             a(32) - a(48) + a(57)
a( 7) =  0.5 * s1 - a(63) - a( 8) - a(64)
a( 6) =           - a(62) + a( 8) + a(64)
a( 5) =             a(62) + a(63) - a( 8)
a( 4) =           - a(60) + a( 8) + a(64)
a( 3) =             a(62) - a( 8) + a(57)
a( 2) =             a(60) - a(62) + a( 8)

The solutions can be obtained by guessing the 8 parameters:

a(i) for i = 32, 48, 56, 60, 62, 63, 8, 57, 64

and filling out these guesses in the abovementioned equations.

The linear equations shown above can be incorporated in a guessing routine, in which the inequalities ensuring Unique Franklin Squares:

a(64) < a(57), a(8), a(1)
a(57) < a(8)

can be incorporated (MgcSqr8f1).

Subject routine counted 1.105.920 Unique Franklin Squares in 16,6 hrs - thus confirming the findings of Schindel, Rempel and Lody - which can be broken down into:

368.640 Pan  Magic Franklin Squares (Most Perfect)
737.280 Semi Magic Franklin Squares

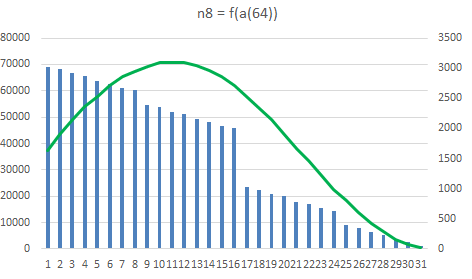
A breakdown of all (Unique) Franklin Squares and the related processor time (green) as a function of a(64) is shown in the graph below:

A dedicated routine for Pan Magic Franklin Squares has been developed and discussed in Section 8.5.3 and returned the same result as mentioned above (368.640 = 2.949.120 / 8).

8.4.4 Additional Properties

As mentioned in section 8.4.1 above, the fourth property (the four corner numbers together with the four middle numbers sum to the Magic Constant) is a consequence of the fifth property ( every 2 × 2 sub square sums to half the Magic Constant).

Starting with the pattern A(8,8) described in the fourth property, other comparable patterns which will sum to the Magic Constant can be recognized:

The indices of pattern A(i,j) should be read as i = rowspan and j = columnspan with i ≠ 2 and j ≠ 2. Note that A(2,2) has been excluded from this definition, as it would lead to a contradiction.

The pattern A(2 ,2) can be considered (definition) as the complementary pattern of A(8,8) and – starting with this pattern B(8,8) = A(2,2) = A_c(8,8) other comparable patterns which will sum to the Magic Constant can be recognized (ref. Attachment 8.4.3).

All these patterns can be translated (with wrap-around) in either direction.

According to certain sources Franklin noted that the "shortened bent rows" plus the "corners" sum also to the Magic Sum 260.

This might have been misunderstood as for the Franklin Square presented above this is only thru for the shortened bent rows which can be moved vertically where for other known squares this is only thru for the shortened bent rows which can be moved horizontally.

However following symmetrical pattern, based on shortened bent rows and corner points, sums to two times the Magic Sum
(= 520):

52	61	4	13	20	29	36	45
14	3	62	51	46	35	30	19
53	60	5	12	21	28	37	44
11	6	59	54	43	38	27	22
55	58	7	10	23	26	39	42
9	8	57	56	41	40	25	24
50	63	2	15	18	31	34	47
16	1	64	49	48	33	32	17

This and comparable patterns can be translated (with wrap-around) in either direction.

8.4.5 Barink Restrictions

In section 12.1 Pan Magic Squares of the 12^th order will be treated, which are constructed by Barink.

One of the defining properties of these squares is that any 4 consecutive numbers starting on any odd place in a row or column sum to one third of the Magic Constant.

A comparable condition applied on the Franklin Squares described in section 8.4.1 above, will limit the number of squares considerable.

For 8^th order squares this condition is that any 4 consecutive numbers starting on any odd place in a row or column sum to one half of the Magic Constant.

For i = 1 and 5 (i = row or column number) this is already covered by the property that every half-row and half-column sums to half the Magic Constant. The remaining equations, which should be added to the equations shown in section 8.4.2 above, are:

The resulting number of equations can be written in the matrix representation as:

           →   →
     A_F2 * a = s

which can be reduced, by means of row and column manipulations, and results in following set of linear equations:

a(61) =  0.5 * s1 - a(62) - a(63) - a(64)
a(59) =           - a(60) + a(63) + a(64)
a(58) =           - a(60) + a(62) + a(64)
a(57) =  0.5 * s1 + a(60) - a(62) - a(63) - 2 * a(64)
a(55) =  0.5 * s1 - a(56) - a(63) - a(64)
a(54) =             a(56) - a(62) + a(64)
a(53) =           - a(56) + a(62) + a(63)
a(52) =             a(56) - a(60) + a(64)
a(51) =  0.5 * s1 - a(56) + a(60) - a(63) - 2 * a(64)
a(50) =             a(56) + a(60) - a(62)
a(49) =           - a(56) - a(60) + a(62) + a(63) + a(64)
a(47) =           - a(48) + a(63) + a(64)
a(46) =             a(48) + a(62) - a(64)
a(45) =  0.5 * s1 - a(48) - a(62) - a(63)
a(44) =             a(48) + a(60) - a(64)
a(43) =           - a(48) - a(60) + a(63) + 2 * a(64)
a(42) =             a(48) - a(60) + a(62)
a(41) =  0.5 * s1 - a(48) + a(60) - a(62) - a(63) - a(64)
a(40) =  0.5 * s1 - a(48) - a(56) - a(64)
a(39) =             a(48) + a(56) - a(63)
a(38) =  0.5 * s1 - a(48) - a(56) - a(62)
a(37) = -0.5 * s1 + a(48) + a(56) + a(62) + a(63) + a(64)
a(36) =  0.5 * s1 - a(48) - a(56) - a(60)
a(35) =             a(48) + a(56) + a(60) - a(63) - a(64)
a(34) =  0.5 * s1 - a(48) - a(56) + a(60) - a(62) - a(64)
a(33) = -0.5 * s1 + a(48) + a(56) - a(60) + a(62) + a(63) + 2 * a(64)
a(31) =           - a(32) + a(63) + a(64)
a(30) =             a(32) + a(62) - a(64)
a(29) =  0.5 * s1 - a(32) - a(62) - a(63)
a(28) =             a(32) + a(60) - a(64)
a(27) =           - a(32) - a(60) + a(63) + 2 * a(64)
a(26) =             a(32) - a(60) + a(62)
a(25) =  0.5 * s1 - a(32) + a(60) - a(62) - a(63) - a(64)
a(24) =           - a(32) + a(56) + a(64)
a(23) =  0.5 * s1 + a(32) - a(56) - a(63) - 2 * a(64)
a(22) =           - a(32) + a(56) - a(62) + 2 * a(64)
a(21) =             a(32) - a(56) + a(62) + a(63) - a(64)
a(20) =           - a(32) + a(56) - a(60) + 2 * a(64)
a(19) =  0.5 * s1 + a(32) - a(56) + a(60) - a(63) - 3 * a(64)
a(18) =           - a(32) + a(56) + a(60) - a(62) + a(64)
a(17) =             a(32) - a(56) - a(60) + a(62) + a(63)
a(16) =           - a(32) + a(48) + a(64)
a(15) =             a(32) - a(48) + a(63)
a(14) =           - a(32) + a(48) + a(62)
a(13) =  0.5 * s1 + a(32) - a(48) - a(62) - a(63) - a(64)
a(12) =           - a(32) + a(48) + a(60)
a(11) =             a(32) - a(48) - a(60) + a(63) + a(64)
a(10) =           - a(32) + a(48) - a(60) + a(62) + a(64)
a( 9) =  0.5 * s1 + a(32) - a(48) + a(60) - a(62) - a(63) - 2 * a(64)
a( 8) =  0.5 * s1 + a(32) - a(48) - a(56) - 2 * a(64)
a( 7) =           - a(32) + a(48) + a(56) - a(63) + a(64)
a( 6) =  0.5 * s1 + a(32) - a(48) - a(56) - a(62) - a(64)
a( 5) = -0.5 * s1 - a(32) + a(48) + a(56) + a(62) + a(63) + 2 * a(64)
a( 4) =  0.5 * s1 + a(32) - a(48) - a(56) - a(60) - a(64)
a( 3) =           - a(32) + a(48) + a(56) + a(60) - a(63)
a( 2) =  0.5 * s1 + a(32) - a(48) - a(56) + a(60) - a(62) - 2 * a(64)
a( 1) = -0.5 * s1 - a(32) + a(48) + a(56) - a(60) + a(62) + a(63) + 3 * a(64)

The solutions can be obtained by guessing a(32), a(48), a(56), a(60) and a(62) ... a(64) and filling out these guesses in the abovementioned equations.

For distinct integers also following inequalities should be applied:

0 < a(i) =< 64        for i = 1, 2, ... 31, 33 ... 47, 49 ... 55, 57, 58, 59 and 61
a(i) ≠ a(j)           for i ≠ j

With a(64) = 17 and a(63) = 40 an optimized guessing routine (MgcSqr8f2), produced 480 Franklin Squares with Barink Restrictions within 56 seconds, which are shown in Attachment 8.4.4.

The total number of order 8 Franklin Squares under the Barink Restrictions is 230.400 (= 8 * 28.800).

8.4.6 Spreadsheet Solutions

The linear equations deducted above, have been applied in following Excel Spread Sheets:

• CnstrSngl8f,  Franklin Squares of order 8
  
  
• CnstrSngl8f2, Franklin Squares of order 8, Barink Restrictions

Only the red figures have to be “guessed” to construct one of the applicable Franklin Squares of the 8^th order (wrong solutions are obvious).