Office Applications and Entertainment, Magic Cubes

7.0    Special Cubes, Prime Numbers

7.11   Magic Cubes, Sum of Latin Cubes (2)

7.11.1 Introduction

As illustrated in Attachment 7.10.3, order 8 Composed Magic Squares can be based on the four horizontal Magic Planes of order 4 Magic Cubes.

Consequently Prime Number Magic Cubes might be constructed based on two suitable selected Latin Cubes, Comparable with order 8 Prime Number Magic Squares (ref. Section 14.12.5).

7.11.2 Simple Magic Cubes (4 x 4 x 4)

The elements of two Latin Cubes A and B, with latin space diagoanls, might result in a Simple Prime Number Magic Cube C with elements c_i = a_i + b_i, i = 1 ... 64 as illustrated below for an Associated Magic Cube:

The key to possible solutions is to find Correlated Balanced Magic Lines {a_i, i = 1 ... 8} and {b_j, j = 1 ... 8} such that c_ij = a_i + b_j (i,j = 1 ... 8) are distinct prime numbers (64 ea).

A few of such sets of Correlated Balanced Magic Lines are shown in following table:

Attachment 7.11.2 shows for each set of Correlated Magic Lines shown above, an example of the resulting Prime Number Associated Magic Cubes (MC = s8/2).

7.11.3 Associated Latin Cubes (4 x 4 x 4)

Associated Latin Cubes, can be obtained by applying the linear equations shown in Section 7.2.3.

For Latin Cubes based on the integers {0, 1 ... 7} the related Magic Sum s1 = 28/2 = 14.

Based on the equations mentioned above, a fast routine can be written to generate the defined Associated Latin Cubes of order 4 (ref. LtnCbs4d1).

Subject routine produced, with a(64) = 0 and a(63) = 1 ... 3, 12240 Associated Latin Cubes within 267 seconds.

Prime Number Associated Magic Cubes C can be generated by selecting combinations of Latin Cubes (A, B) while:

• substituting the integers {0, 1 ... 7} by {a_i, i = 1 ... 8} and {b_j, j = 1 ... 8};
• ensuring that for the resulting cube C the numbers c_ij = a_i + b_j (i,j = 1 ... 8) are distinct prime numbers (64 ea).

which can be achieved with routine CnstrCbs4b.

Due to the vast amount of Associated Latin Cubes, a more controllable collection of Associated Magic Cubes can be obtained by means of Self Orthogonal Latin Cubes.

The principle is illustrated below for the equivalent order 8 Latin Squares of the Associated Latin - and resulting Magic Cubes shown in Section 7.11.2 above.

Square A8 is Semi-Latin with Latin Rows and Latin Diagonals (Symmetrical). The Semi-Latin Square B8 is the transposed square of A8 (rows and columns exchanged).

Based on this principle, a routine can be written to generate Prime Number Associated Magic Cubes of order 4 (ref. LtnCbs4d2).

Subject routine counted 2304 Prime Number Assocociated Magic Cubes within an hour (MC = 12012), of wich 32 are shown in Attachment 7.11.3.

Attachment 7.11.2 shows for each set of Correlated Magic Lines shown in Section 7.10.2 above, an example of the resulting Prime Number Associated Magic Cubes.

7.11.4 Associated Latin Cubes (4 x 4 x 4)
       3D Compact

Associated, 3D Compact Latin Cubes can be obtained by the linear equations shown in Section 7.2.4.

For Latin Cubes based on the integers {0, 1 ... 7} the related Magic Sum s1 = 28/2 = 14.

Based on the equations mentioned above, a fast routine can be written to generate the defined Associated Latin Cubes of order 4 (ref. LtnCbs44).

Subject routine produced 6528 (= 17 * 384) Associated, 3D Compact Latin Cubes within 45 seconds.

Based on this collection, 2.654.208 Associated, 3D Compact Magic Cubes can be constructed (ref. CnstrCbs4b).

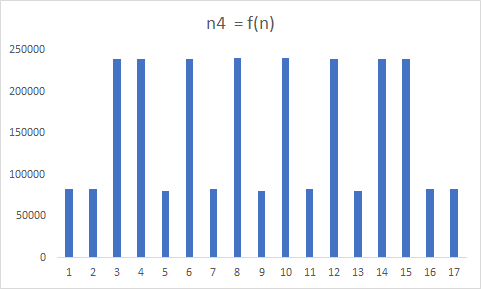
The graph shown above, shows the frequency n4 of subject Associated, 3D Compact Magic Cubes as a function of n (multiples of 384).

Attachment 7.11.4 shows for each set of Correlated Magic Lines shown in Section 7.10.2 above, an example of the resulting Prime Number Associated, 3D Compact Magic Cubes.

7.11.5 Simple Latin Cubes (4 x 4 x 4)
       Horizontal Associated Magic Planes

Simple Latin Cubes with Horizontal Associated Planes can be obtained by applying the linear equations shown in Section 7.2.2.

For Latin Cubes based on the integers {0, 1 ... 7} the related Magic Sum s1 = 28/2 = 14.

Based on the equations mentioned above, a fast routine can be written to generate the defined Simple Latin Cubes of order 4 (ref. LtnCbs41).

Subject routine produced 768 Simple Latin Cubes with Horizontal Associated Magic Planes within 17 seconds.

Based on this collection, 294912 Magic Cubes with Horizontal Associated Magic Planes can be constructed (ref. CnstrCbs4b).

Attachment 7.11.5 shows for each set of Correlated Magic Lines shown in Section 7.10.2 above, an example of the resulting Prime Number Simple Magic Cubes with Horizontal Associated Magic Planes.

7.11.6 Simple Latin Cubes (4 x 4 x 4)
       Horizontal Pan Magic Planes

Simple Latin Cubes with Horizontal Pan Magic Planes can be obtained by applying the linear equations shown in Section 7.2.1.

For Latin Cubes based on the integers {0, 1 ... 7} the related Magic Sum s1 = 28/2 = 14.

Based on the equations mentioned above, a fast routine can be written to generate the defined Simple Latin Cubes of order 4 (ref. LtnCbs42).

Subject routine produced 1536 Simple Latin Cubes with Horizontal Pan Magic Planes within 7,7 seconds.

Based on this collection, 589824 Magic Cubes with Horizontal Pan Magic Planes can be constructed (ref. CnstrCbs4b).

Attachment 7.11.6 shows for each set of Correlated Magic Lines shown in Section 7.10.2 above, an example of the resulting Prime Number Simple Magic Cubes with Horizontal Pan Magic Planes.

7.11.7 Simple Latin Cubes (4 x 4 x 4)
       Pantriagonal and Complete

Pantriagonal and Complete (Semi) Latin Cubes can be obtained by applying the linear equations shown in Section 7.2.6.

For (Semi) Latin Cubes based on the integers {0, 1 ... 7} the related Magic Sum s1 = 28/2 = 14.

Based on the equations mentioned above, a fast routine can be written to generate the defined Simple (Semi) Latin Cubes of order 4 (ref. LtnCbs46).

Subject routine produced 53760 Pantriagonal and Complete (Semi) Latin Cubes within 529 seconds.

Based on the sub collection of the first 1268 (Semi) Latin Cubes, 1440 Pantriagonal and Complete Magic Cubes can be constructed (ref. CnstrCbs4b).

Attachment 7.11.7 shows for each set of Correlated Magic Lines shown in Section 7.10.2 above, an example of the resulting Prime Number Pantriagonal and Complete Magic Cubes.

7.11.8 Summary

The obtained results regarding the miscellaneous Prime Number Magic Cubes as deducted and discussed in previous sections are summarized in following table:

This is the end of the Chapter 'Prime Number Magic Cubes' of this website.