Office Applications and Entertainment, Magic Cubes | ||
|
|
Index | About the Author |
|
1.0 Introduction
Comparable with Magic Squares as discussed on this Website,
Magic Cubes of order n can be defined as arrangements of n3 numbers, usually distinct integers, in cubes, such that the n numbers in all rows, columns, pillars and all or a part of the plane - and space diagonals sum to the same constant.
2.0 Magic Cubes (3 x 3 x 3)
The first 3 x 3 x 3 Magic Cube was published by T. Hugel in 1876.
All rows, columns, pillars and 4 space diagonals sum to 42.
|
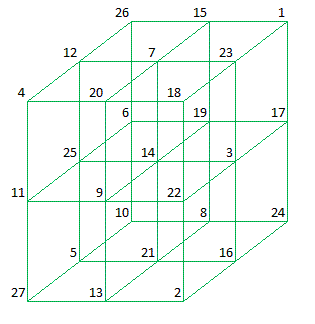
Plane 3
26
15
1
12
7
23
4
20
18
Plane 2
6
19
17
25
14
3
11
9
22
Plane 1
10
8
24
5
21
16
27
13
2
|
Plane 1, 2 and 3 are respectively the bottom -, the middle - and the top square. It should be noted that Plane 1 and 3 are
semi magic and only Plane 2 is magic.
In general Magic Cubes of order 3 can be represented as follows:
|
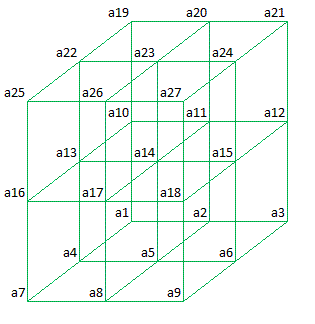
Plane 3
a19
a20
a21
a22
a23
a24
a25
a26
a27
Plane 2
a10
a11
a12
a13
a14
a15
a16
a17
a18
Plane 1
a1
a2
a3
a4
a5
a6
a7
a8
a9
|
As the numbers a(i), i = 1 ... 27, in all rows, columns, pillars and space diagonals sum to the same constant this results in following linear equations:
|
|
|
Rows
|
Columns
|
Diagonals
|
|
Plane 1
|
a1 + a4 + a7 = 42 |
a1 + a2 + a3 = 42 |
|
|
Plane 2
|
a10 + a13 + a16 = 42 |
a10 + a11 + a12 = 42 |
a10 + a14 + a18 = 42 |
|
Plane 3
|
a19 + a22 + a25 = 42 |
a19 + a20 + a21 = 42 |
|
|
Pillars
|
a1 + a10 + a19 = 42 |
a2 + a11 + a20 = 42 |
a3 + a12 + a21 = 42 |
|
Space Diagonals
|
a1 + a14 + a27 = 42 |
a3 + a14 + a25 = 42 |
|
|
which results in following minimum number of linear equations:
a(25) = 42 - a(26) - a(27)
Abovementioned reduction is achieved by means of a VBA for Excel procedure (Algorithm3), based on reduction algorithms
Rotation:
The linear equations deducted in Section 2.2 above, can be applied in an Excel spreadsheet (ref. CnstrSngl3).
|
|
|
Index | About the Author |