Office Applications and Entertainment, Magic Cubes

3.0 Magic Cubes (4 x 4 x 4)

3.1 Historical Background

Magic Cubes as discussed in section 2.1 for which not all diagonals sum to the Magic Constant are normally referred to as Simple Magic Cubes.

A more strict defined Class of Magic Cubes is known as ‘Perfect Magic Cubes’, for which all (6n + 4) diagonals sum to the Magic Sum.

For 4 x 4 x 4 Magic Cubes it has been proven that Perfect Magic Cubes are impossible (refer also section 3.3).

However in 2004 Walter Trump found a cube that is almost a Perfect Magic Cube, as all rows, columns, pillars and diagonals with exception of the space diagonals sum to the Magic Sum.

The cube and the 12 orthogonal planes are shown below:

Each of the 12 orthogonal planes contain a Non Normal Magic Square, meaning the Magic Squares contain distinct but not consecutive integers. In addition to this the cube is plane symmetrical (horizontal planes).

The cube belongs to a Class of 48 elements which can be found by means of rotation and/or reflection which is visualised in Attachment 3.1.3 and Attachment 3.1.4.

3.2 Analytic Solution

In general Magic Cubes of order 4 can be represented as follows:

As the numbers a(i), i = 1 ... 64 for each of the rows, columns and (long) plane diagonals of the 12 orthogonal planes sum to the same constant (130) this results in following linear equations:

Plane 11 (Top)

a(49)+a(50)+a(51)+a(52) = 130
a(53)+a(54)+a(55)+a(56) = 130
a(57)+a(58)+a(59)+a(60) = 130
a(61)+a(62)+a(63)+a(64) = 130

a(49)+a(53)+a(57)+a(61) = 130
a(50)+a(54)+a(58)+a(62) = 130
a(51)+a(55)+a(59)+a(63) = 130
a(52)+a(56)+a(60)+a(64) = 130

a(49)+a(54)+a(59)+a(64) = 130
a(52)+a(55)+a(58)+a(61) = 130

Plane 21 (Left)

a(61)+a(57)+a(53)+a(49) = 130
a(45)+a(41)+a(37)+a(33) = 130
a(29)+a(25)+a(21)+a(17) = 130
a(13)+a(9 )+a(5 )+a( 1) = 130

a(61)+a(45)+a(29)+a(13) = 130
a(57)+a(41)+a(25)+a( 9) = 130
a(53)+a(37)+a(21)+a( 5) = 130
a(49)+a(33)+a(17)+a( 1) = 130

a(61)+a(41)+a(21)+a( 1) = 130
a(49)+a(37)+a(25)+a(13) = 130

Plane 31 (Back)

a(49)+a(50)+a(51)+a(52) = 130
a(33)+a(34)+a(35)+a(36) = 130
a(17)+a(18)+a(19)+a(20) = 130
a( 1)+a( 2)+a( 3)+a( 4) = 130

a(49)+a(33)+a(17)+a( 1) = 130
a(50)+a(34)+a(18)+a( 2) = 130
a(51)+a(35)+a(19)+a( 3) = 130
a(52)+a(36)+a(20)+a( 4) = 130

a(49)+a(34)+a(19)+a( 4) = 130
a(52)+a(35)+a(18)+a( 1) = 130

Plane 12

a(33)+a(34)+a(35)+a(36) = 130
a(37)+a(38)+a(39)+a(40) = 130
a(41)+a(42)+a(43)+a(44) = 130
a(45)+a(46)+a(47)+a(48) = 130

a(33)+a(37)+a(41)+a(45) = 130
a(34)+a(38)+a(42)+a(46) = 130
a(35)+a(39)+a(43)+a(47) = 130
a(36)+a(40)+a(44)+a(48) = 130

a(33)+a(38)+a(43)+a(48) = 130
a(36)+a(39)+a(42)+a(45) = 130

Plane 22

a(62)+a(58)+a(54)+a(50) = 130
a(46)+a(42)+a(38)+a(34) = 130
a(30)+a(26)+a(22)+a(18) = 130
a(14)+a(10)+a( 6)+a( 2) = 130

a(62)+a(46)+a(30)+a(14) = 130
a(58)+a(42)+a(26)+a(10) = 130
a(54)+a(38)+a(22)+a( 6) = 130
a(50)+a(34)+a(18)+a( 2) = 130

a(62)+a(42)+a(22)+a( 2) = 130
a(50)+a(38)+a(26)+a(14) = 130

Plane 32

a(53)+a(54)+a(55)+a(56) = 130
a(37)+a(38)+a(39)+a(40) = 130
a(21)+a(22)+a(23)+a(24) = 130
a( 5)+a( 6)+a( 7)+a( 8) = 130

a(53)+a(37)+a(21)+a( 5) = 130
a(54)+a(38)+a(22)+a( 6) = 130
a(55)+a(39)+a(23)+a( 7) = 130
a(56)+a(40)+a(24)+a( 8) = 130

a(53)+a(38)+a(23)+a( 8) = 130
a(56)+a(39)+a(22)+a( 5) = 130

Plane 13

a(17)+a(18)+a(19)+a(20) = 130
a(21)+a(22)+a(23)+a(24) = 130
a(25)+a(26)+a(27)+a(28) = 130
a(29)+a(30)+a(31)+a(32) = 130

a(17)+a(21)+a(25)+a(29) = 130
a(18)+a(22)+a(26)+a(30) = 130
a(19)+a(23)+a(27)+a(31) = 130
a(20)+a(24)+a(28)+a(32) = 130

a(17)+a(22)+a(27)+a(32) = 130
a(20)+a(23)+a(26)+a(29) = 130

Plane 23

a(63)+a(59)+a(55)+a(51) = 130
a(47)+a(43)+a(39)+a(35) = 130
a(31)+a(27)+a(23)+a(19) = 130
a(15)+a(11)+a( 7)+a( 3) = 130

a(63)+a(47)+a(31)+a(15) = 130
a(59)+a(43)+a(27)+a(11) = 130
a(55)+a(39)+a(23)+a( 7) = 130
a(51)+a(35)+a(19)+a( 3) = 130

a(63)+a(43)+a(23)+a( 3) = 130
a(51)+a(39)+a(27)+a(15) = 130

Plane 33

a(57)+a(58)+a(59)+a(60) = 130
a(41)+a(42)+a(43)+a(44) = 130
a(25)+a(26)+a(27)+a(28) = 130
a( 9)+a(10)+a(11)+a(12) = 130

a(57)+a(41)+a(25)+a( 9) = 130
a(58)+a(42)+a(26)+a(10) = 130
a(59)+a(43)+a(27)+a(11) = 130
a(60)+a(44)+a(28)+a(12) = 130

a(57)+a(42)+a(27)+a(12) = 130
a(60)+a(43)+a(26)+a( 9) = 130

Plane 14

a( 1)+a( 2)+a( 3)+a( 4) = 130
a( 5)+a( 6)+a( 7)+a( 8) = 130
a( 9)+a(10)+a(11)+a(12) = 130
a(13)+a(14)+a(15)+a(16) = 130

a( 1)+a( 5)+a( 9)+a(13) = 130
a( 2)+a( 6)+a(10)+a(14) = 130
a( 3)+a( 7)+a(11)+a(15) = 130
a( 4)+a( 8)+a(12)+a(16) = 130

a( 1)+a( 6)+a(11)+a(16) = 130
a( 4)+a( 7)+a(10)+a(13) = 130

Plane 24

a(64)+a(60)+a(56)+a(52) = 130
a(48)+a(44)+a(40)+a(36) = 130
a(32)+a(28)+a(24)+a(20) = 130
a(16)+a(12)+a( 8)+a( 4) = 130

a(64)+a(48)+a(32)+a(16) = 130
a(60)+a(44)+a(28)+a(12) = 130
a(56)+a(40)+a(24)+a( 8) = 130
a(52)+a(36)+a(20)+a( 4) = 130

a(64)+a(44)+a(24)+a( 4) = 130
a(52)+a(40)+a(28)+a(16) = 130

Plane 34

a(61)+a(62)+a(63)+a(64) = 130
a(45)+a(46)+a(47)+a(48) = 130
a(29)+a(30)+a(31)+a(32) = 130
a(13)+a(14)+a(15)+a(16) = 130

a(61)+a(45)+a(29)+a(13) = 130
a(62)+a(46)+a(30)+a(14) = 130
a(63)+a(47)+a(31)+a(15) = 130
a(64)+a(48)+a(32)+a(16) = 130

a(61)+a(46)+a(31)+a(16) = 130
a(64)+a(47)+a(30)+a(13) = 130

a(1) + a(49) = 65
a(2) + a(50) = 65
a(3) + a(51) = 65
a(4) + a(52) = 65
a(5) + a(53) = 65
a(6) + a(54) = 65
a(7) + a(55) = 65
a(8) + a(56) = 65

a( 9) + a(57) = 65
a(10) + a(58) = 65
a(11) + a(59) = 65
a(12) + a(60) = 65
a(13) + a(61) = 65
a(14) + a(62) = 65
a(15) + a(63) = 65
a(16) + a(64) = 65

a(17) + a(33) = 65
a(18) + a(34) = 65
a(19) + a(35) = 65
a(20) + a(36) = 65
a(21) + a(37) = 65
a(22) + a(38) = 65
a(23) + a(39) = 65
a(24) + a(40) = 65

a(25) + a(41) = 65
a(26) + a(42) = 65
a(27) + a(43) = 65
a(28) + a(44) = 65
a(29) + a(45) = 65
a(30) + a(46) = 65
a(31) + a(47) = 65
a(32) + a(48) = 65

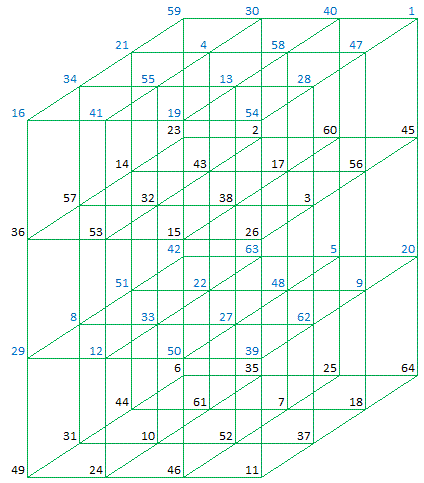
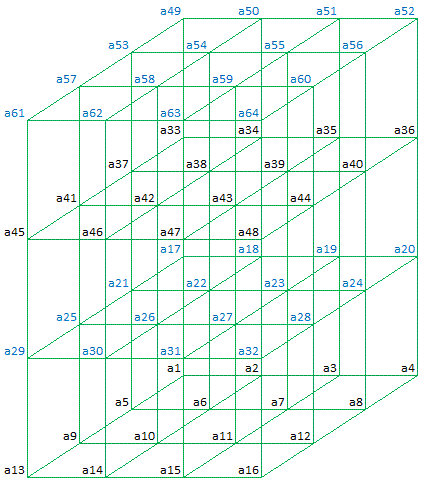
which results, after deduction, in following set of linear equations describing the 'Almost Perfect Magic Cubes' as found by Walter Trump:

a(61) = 130 - a(62) - a(63) - a(64)
a(57) = 130 - a(58) - a(59) - a(60)
a(56) =  65 + a(58) - a(63) - a(64)
a(55) = -65 + a(60) + a(62) + a(64)
a(54) = 130 - a(55) - a(58) - a(59)
a(53) = -65 + a(59) + a(63) + a(64)
a(52) =  65 - a(58) - a(60) + a(63)
a(51) = 130 - a(53) - a(60) - a(62)
a(50) = -65 + a(59) + a(60) + a(64)
a(49) = -65 + a(58) + a(60) + a(62)
a(46) =       a(47) - a(61) + a(64)
a(45) = 130 - a(46) - a(47) - a(48)
a(44) = 130 - a(47) - a(48) - 0.5 * a(58) + 0.5 * a(59) - 0.5 * a(62) + 0.5 * a(63) - a(64)
a(43) = 260 - a(44) - a(47) - a(48) - a(58) - a(60) - a(62) - a(64)
a(42) = 130 - a(43) - a(62) - a(63)
a(41) =     - a(44) + a(62) + a(63)
a(40) =  65 + a(42) - a(47) - a(48)
a(39) =  65 - a(41) + a(47) + a(48) - 2 * a(61)
a(38) =     - a(39) + a(62) + a(63)
a(37) = 130 - a(40) - a(62) - a(63)
a(36) = 130 - a(40) - a(44) - a(48)
a(35) = 130 - a(39) - a(43) - a(47)
a(34) = 130 - a(35) - 2 * a(47) + a(61) - a(64)
a(33) = 130 - a(48) - a(51) - a(62)

The linear equations shown above, are ready to be solved, for the Magic Constant 130.

The solutions can be obtained by guessing:

   a(47), a(48), a(58) ... a(60) and a(62) ... a(64)

and filling out these guesses in the abovementioned equations.

For distinct integers also following relations are applicable:

0 < a(i) =< 64        for i = 1, 2, ... 46, 49 ... 57 and 61
Int(a(i)) = a(i)      for i = 44
a(i) ≠ a(j)           for i ≠ j

which have been incorporated in an optimized guessing routine (MgcCube4c).

Subject guessing routine produced 184320 (= 64 * 15 * 48 * 4) Magic Cubes within 2.7 hours, of which the first 192 are shown in Attachment 3.2.1 and Attachment 3.2.2.

3.2.2 Almost Perfect Cubes, Generalised

If only the numbers a(i), i = 1 ... 64 for each of the rows, columns and (long) plane diagonals of the 12 orthogonal planes sum to the same constant (130) the linear equations shown in section 3.2 above can be deducted to:

a(61) =  130 - a(62) - a(63) - a(64)
a(57) =  130 - a(58) - a(59) - a(60)
a(55) = -130 + a(56) - a(58) + a(60) + a(62) + a(63) + 2 * a(64)
a(54) =  130 - a(55) - a(58) - a(59)
a(53) =      - a(56) + a(58) + a(59)
a(52) =  130 - a(56) - a(60) - a(64)
a(51) =  130 - a(55) - a(59) - a(63)
a(50) =        a(55) + a(59) - a(62)
a(49) =        a(55) + a(58) - a(64)
a(45) =  130 - a(46) - a(47) - a(48)
a(43) =  130 - a(44) - a(46) - a(48) - a(58) - a(60) + a(63) + a(64)
a(42) =  130 - a(43) - a(62) - a(63)
a(41) =      - a(44) + a(62) + a(63)
a(40) =  130 + a(42) - a(47) - a(48) - a(56) + a(58) - a(63) - a(64)
a(39) =  130 - a(43) - a(56) - a(60)
a(38) =      - a(42) + a(56) + a(60)
a(37) =  130 - a(40) - a(62) - a(63)
a(36) =  130 - a(40) - a(44) - a(48)
a(35) =      - a(47) + a(56) + a(60)
a(34) =  130 - a(46) - a(56) - a(60)
a(33) =      - a(36) + a(46) + a(47)
a(32) =  195 + a(44) + 1.5*a(46) - 0.5*a(47) - a(56) + 1.5*a(58) - 0.5*a(59) - a(62) - 3*a(63) - 3*a(64)
a(31) = -130 + a(32) - a(46) + a(48) + a(62) + a(63) + 2 * a(64)
a(30) =  130 - a(31) - a(46) - a(47)
a(29) =      - a(32) + a(46) + a(47)
a(28) =      - a(30) - a(44) - a(46) + 2 * a(56) - 2 * a(58) + 2 * a(63) + 2 * a(64)
a(27) =      - a(32) + a(44) + a(46) + a(58) + a(60) - a(63) - a(64)
a(26) =      - a(27) + a(62) + a(63)
a(25) =      - a(27) - a(46) - a(48) + a(59) + a(60) + a(63) + a(64)
a(24) =  260 - a(32) - a(44) - a(48) - a(56) - a(60) - 2 * a(64)
a(23) =      - a(27) + a(56) + a(60)
a(22) =  130 - a(23) - a(62) - a(63)
a(21) =      - a(24) + a(62) + a(63)
a(20) =  130 - a(25) + a(44) - a(46) - a(47) - a(48) - a(56) + a(58) + a(59) + a(60) - a(62) - a(63)
a(19) =      - a(21) + a(44) + a(46)
a(18) =        a(21) - a(44) + a(47)
a(17) =  130 - a(20) - a(46) - a(47)
a(16) = -130 - a(18) + a(47) + a(56) + a(60) + a(62) + a(63) + a(64)
a(15) =        a(19) - a(47) + a(56) + a(60) - a(63)
a(14) =  130 - a(15) - a(62) - a(63)
a(13) =      - a(16) + a(62) + a(63)
a(12) =  260 + a(20) - 2 * a(44) - a(48) - a(56) - 2 * a(60) - 2 * a(64)
a(11) =  130 + a(13) - a(59) - a(62) - a(63) - a(64)
a(10) =  130 - a(11) - a(58) - a(59)
a( 9) =      - a(17) + a(48) + a(56)
a( 8) =  130 - a(12) - a(56) - a(60)
a( 7) =      - a( 8) - a(46) + a(47) - a(58) - a(60) + 2 * a(63) + 2 * a(64)
a( 6) = -260 + a(11) + a(56) + 2 * a(59) + a(60) + a(62) + a(63) + 2 * a(64)
a( 5) =  390 - a(12) - 2 * a(44) - a(46) - a(47) - 2 * a(48) - a(56) - a(60) - 2 * a(64)
a( 4) =  130 + a(6) - a(59) - a(62) - a(63) - a(64)
a( 3) =      - a(5) + a(60) + a(62)
a( 2) =      - a(3) + a(62) + a(63)
a( 1) =  130 - a(4) - a(62) - a(63)

The linear equations shown above, are ready to be solved, for the Magic Constant 130.

The solutions can be obtained by guessing:

   a(44), a(46) ... a(48), a(56), a(58) ... a(60) and a(62) ... a(64)

and filling out these guesses in the abovementioned equations.

For distinct integers also following relations are applicable:

0 < a(i) =< 64        for i = 1, 2, ... 43, 45, 49 ... 55, 57 and 61
Int(a(i)) = a(i)      for i = 32
a(i) ≠ a(j)           for i ≠ j

which have been incorporated in an optimized guessing routine (MgcCube4a). Due to the absence of the Plane Symmetrical restrictions this guessing routine appeared to be disappointing slow.

However, the equations deducted above can be applied in a much more efficient method to generate Almost Perfect Magic Cubes, which will be discussed in Section 3.12.

3.3 Perfect Magic Cubes of order 4 don't exist (Alternative Proof)

If the equations for the 4 Space Diagonals:

a(13) + a(26) + a(39) + a(52) = 130
a(16) + a(27) + a(38) + a(49) = 130
a( 1) + a(22) + a(43) + a(64) = 130
a( 4) + a(23) + a(42) + a(61) = 130

are added to the equations of the 'Almost Perfect Magic Cubes', the following set of linear equations will result:

a(62) =   65 - a(63)
a(61) =   65 - a(64)
a(57) =  130 - a(58) - a(59) - a(60)
a(56) =   65 - a(60)
a(55) =      - a(58) + 2 * a(64)
a(54) =  130 - a(59) - 2 * a(64)
a(53) =  -65 + a(58) + a(59) + a(60)
a(52) =   65 - a(64)
a(51) =  130 + a(58) - a(59) - a(63) - 2 * a(64)
a(50) =  -65 - a(58) + a(59) + a(63) + 2 * a(64)
a(49) =        a(64)
a(45) =  130 - a(46) - a(47) - a(48)
a(44) = -1.5 * a(46) + 0.5 * a(47) - a(48) - 1.5 * a(58) + 0.5 * a(59) - a(60) + 2 * a(63) + 3 * a(64)
a(43) =  130 + 0.5 * a(46) - 0.5 * a(47) + 0.5 * a(58) - 0.5 * a(59) - a(63) - 2 * a(64)
a(42) =  -65 - 0.5 * a(46) + 0.5 * a(47) - 0.5 * a(58) + 0.5 * a(59) + a(63) + 2 * a(64)
a(41) =   65 + 1.5 * a(46) - 0.5 * a(47) + a(48) + 1.5 * a(58) - 0.5 * a(59) + a(60) - 2 * a(63) - 3 * a(64)
a(40) =      - 0.5 * a(46) - 0.5 * a(47) - a(48) + 0.5 * a(58) + 0.5 * a(59) + a(60) + a(64)
a(39) =  -65 - 0.5 * a(46) + 0.5 * a(47) - 0.5 * a(58) + 0.5 * a(59) + a(63) + 2 * a(64)
a(38) =  130 + 0.5 * a(46) - 0.5 * a(47) + 0.5 * a(58) - 0.5 * a(59) - a(63) - 2 * a(64)
a(37) =   65 + 0.5 * a(46) + 0.5 * a(47) + a(48) - 0.5 * a(58) - 0.5 * a(59) - a(60) - a(64)
a(36) =  130 + 2 * a(46) + a(48) + a(58) - a(59) - 2 * a(63) - 4 * a(64)
a(35) =   65 - a(47)
a(34) =   65 - a(46)
a(33) = -130 - a(46) + a(47) - a(48) - a(58) + a(59) + 2 * a(63) + 4 * a(64)
a(32) =   65 - a(48)
a(31) =      - a(46) + 2 * a(64)
a(30) =  130 - a(47) - 2 * a(64)
a(29) =  -65 + a(46) + a(47) + a(48)
a(28) =  0.5 * a(46) + 0.5 * a(47) + a(48) - 0.5 * a(58) - 0.5 * a(59) - a(60) + a(64)
a(27) =  -65 - 0.5 * a(46) + 0.5 * a(47) - 0.5 * a(58) + 0.5 * a(59) + a(63) + 2 * a(64)
a(26) =  130 + 0.5 * a(46) - 0.5 * a(47) + 0.5 * a(58) - 0.5 * a(59) - a(63) - 2 * a(64)
a(25) =   65 - 0.5 * a(46) - 0.5 * a(47) - a(48) + 0.5 * a(58) + 0.5 * a(59) + a(60) - a(64)
a(24) =  130 + 1.5 * a(46) - 0.5 * a(47) + a(48) + 1.5 * a(58) - 0.5 * a(59) + a(60) - 2 * a(63) - 5 * a(64)
a(23) =  130 + 0.5 * a(46) - 0.5 * a(47) + 0.5 * a(58) - 0.5 * a(59) - a(63) - 2 * a(64)
a(22) =  -65 - 0.5 * a(46) + 0.5 * a(47) - 0.5 * a(58) + 0.5 * a(59) + a(63) + 2 * a(64)
a(21) =  -65 - 1.5 * a(46) + 0.5 * a(47) - a(48) - 1.5 * a(58) + 0.5 * a(59) - a(60) + 2 * a(63) + 5 * a(64)
a(20) =  -65 - 2 * a(46) - a(48) - a(58) + a(59) + 2 * a(63) + 4 * a(64)
a(19) =   65 + a(46) - 2 * a(64)
a(18) =  -65 + a(47) + 2 * a(64)
a(17) =  195 + a(46) - a(47) + a(48) + a(58) - a(59) - 2 * a(63) - 4 * a(64)
a(16) =   65 - a(64)
a(15) =  130 + a(46) - a(47) - a(63) - 2 * a(64)
a(14) =  -65 - a(46) + a(47) + a(63) + 2 * a(64)
a(13) =        a(64)
a(12) =  130 + a(46) - a(47) + 2 * a(58) + a(60) - 2 * a(63) - 4 * a(64)
a(11) =   65 - a(59)
a(10) =   65 - a(58)
a( 9) = -130 - a(46) + a(47) - a(58) + a(59) - a(60) + 2 * a(63) + 4 * a(64)
a( 8) =  -65 - a(46) + a(47) - 2 * a(58) - a(60) + 2 * a(63) + 4 * a(64)
a( 7) =   65 + a(58) - 2 * a(64)
a( 6) =  -65 + a(59) + 2 * a(64)
a( 5) =  195 + a(46) - a(47) + a(58) - a(59) + a(60) - 2 * a(63) - 4 * a(64)
a( 4) =        a(64)
a( 3) = -130 - a(46) + a(47) - a(58) + a(59) + a(63) + 4 * a(64)
a( 2) =  195 + a(46) - a(47) + a(58) - a(59) - a(63) - 4 * a(64)
a( 1) =   65 - a(64)

The equations above will definitely not return sets of distinct integers as:

   a( 1) = a(16) = a(52) = a(61)
   a( 4) = a(13) = a(49) = a(64)
   a(22) = a(27) = a(39) = a(42)
   a(23) = a(26) = a(38) = a(43)

Consequently Perfect Magic Cubes of the 4^th order don’t exist.

The same method can be used to proof that 4^th order Magic Cubes with Pan Magic Orthogonal Squares don’t exist either.