Office Applications and Entertainment, Magic Squares

10.5   Construction Methods, Non Consecutive Integers

10.5.1 Introduction

Although, as mentioned in Section 6.1 Pan Magic Squares of order (4n + 2) - based on consecutive distinct integers - don't exist it is possible to construct individual Pan Magic Squares of order 10, with non consecutive integers.

The method discussed in Section 10.5.2 below, is quite comparable with the method discussed in Section 13.4 for the construction of double even Pan Magic Squares.

10.5.2 Associated, Compact, Pan Magic

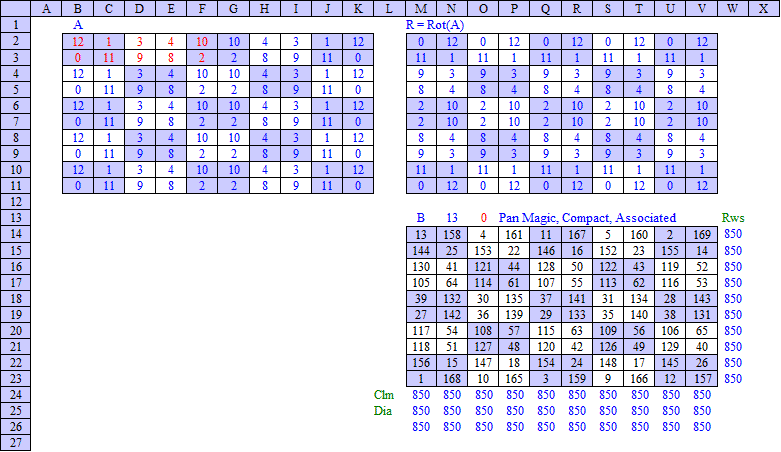
Associated Compact Pan Magic Squares of order 10 can be constructed by means of following method:

1. Fill the first 5 columns of the first 2 rows of square A with 10 different natural numbers 0, 1, ... m, in such a way that:
   - Each vertical pair has the same sum s1/5
   - Both half rows have the same sum s1/2
   with s1 the sum of the 10 numbers used. Examples will be deducted in Section 10.5.4 below.
2. Copy the resulting 2 × 5 rectangle 4 times under the first rectangle;
3. Copy the resulting left 10 × 5 rectangle, horizontal reflected, into the right 10 × 5 rectangle;
4. Construct a second square R by means of 90^o rotation of square A;
5. Construct square B by means of the matrix operation B = (m + n + 1) * R + A + [1] with n = 0, 1, ... .

As an example, subject method has been applied in an Excel spreadsheet for s1 = 60 and n = 0, which results in an Associated Compact Pan Magic Square of order 10 with Magic Sum MC = 850, as shown below:

Based on the resulting variable values {b_i}, numerous Associated Compact Pan Magic Squares can be generated with routine MgcSqr10e.

10.5.3 Compact, Pan Magic, Complete

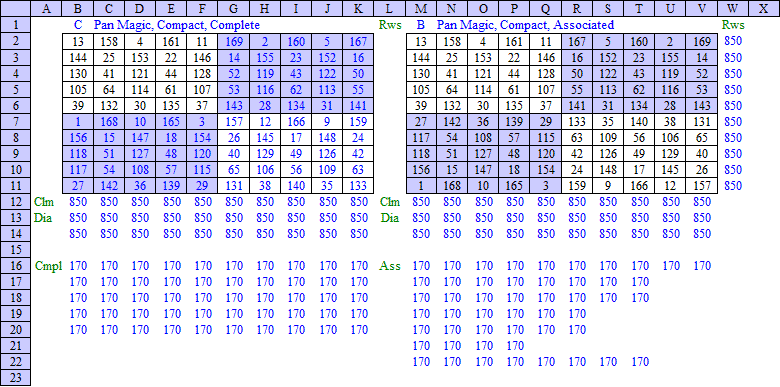
A Compact Complete Pan Magic Square C can be constructed based on an Associated Compact Magic Square B as constructed above by applying following transformation (Euler):

1. Divide square B into four 5 x 5 sub squares:
   - B11 left top;
   - B12 right top;
   - B21 left bottom and
   - B22 right bottom.
2. Fill the corresponding sub squares of C as follows:
   - C11 = B11;
   - C12 = B12, horizontal reflected;
   - C21 = B21, vertical reflected;
   - C22 = B22, rotated 180^o.

As an example, subject method has been applied in an Excel spreadsheet on the Associated Compact Pan Magic Square B constructed in Section 10.5.2, as shown below:

It is also possible to generate numerous Most Perfect Pan Magic Squares based on the obtained variable values {b_i} directly with routine MgcSqr10d.

10.5.4 Miscellaneous Magic Sums

The equations defining 2 x 5 Magic Rectangles for which the 10 elements sum to s1 are:

a(6) = s1/2 - a(7) - a(8) - a(9) - a(10)
a(5) = s1/5 - a(10)
a(4) = s1/5 - a(9)
a(3) = s1/5 - a(8)
a(2) = s1/5 - a(7)
a(1) = s1/5 - a(6)

with a(7), a(8), a(9) and a(10) the independent variables. Consequently the sum of the variables s1 should be divisible by 2 * 5 = 10.

Based on the equations above a routine can be written to generate subject Magic Rectangles for miscellaneous variable sets {a_i} and sums s1 (ref. MgcSqr52).

Attachment 10.4.4 shows for s1 = 60, 70, 80 one Magic Rectangle per related variable set {a_i}. Each rectangle shown corresponds with 240 Magic Rectangles.