Office Applications and Entertainment, Magic Cubes

4.6 Analytic Solution Almost Perfect Center Symmetric Magic Cubes

About a century before the 5^th order Perfect Magic Cube was published, following Almost Perfect Center Symmetric Magic Cube was published by Andrews (1908):

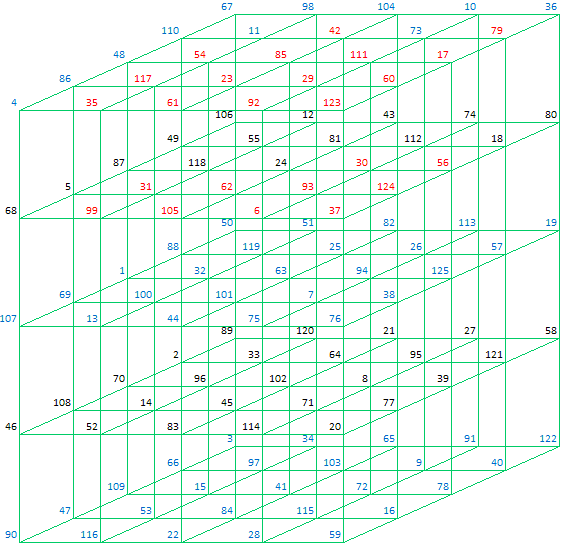
Plane 11 (Top)

Plane 12

Plane 13

Plane 14

Plane 15

The defining properties of an Almost Perfect Center Symmetric Cube of the fifth order can be summarised as follows:

• The Rows (25), Columns (25), Pillars (25) and Space Diagonals (4) sum to the Magic Sum (315);
  
  
• The Main Diagonals of the horizontal planes sum to the Magic Sum (315);
  
  
• For both sets vertical planes 6 out of 10 Main Diagonals sum to the Magic Sum (315);
  
  
• The equations for Center Symmetrical Cubes are applicable

Although this definition depends from the orientation of the cube, this will be used as a guideline in the equations below.

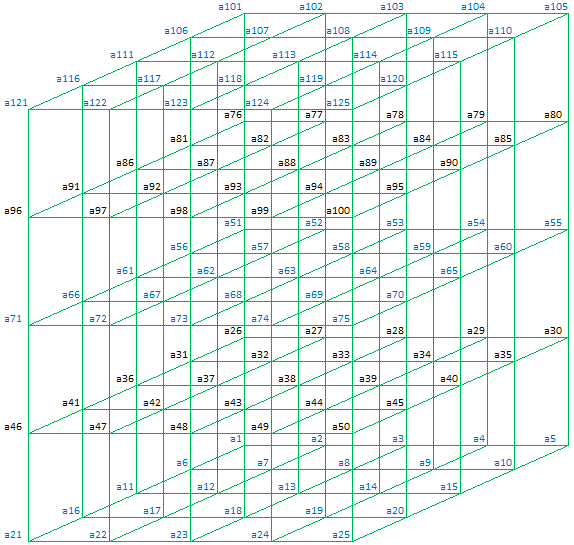
Plane 11 (Top)

Plane 12

Plane 13

Plane 14

Plane 15

After deduction of the defining equations, the following set of linear equations - describing the Almost Perfect Center Symmetric Cubes of the 5^th order - can be obtained:

a121 =     s1 - a122 - a123 - a124 - a125
a116 =     s1 - a117 - a118 - a119 - a120
a111 =     s1 - a112 - a113 - a114 - a115
a109 =          a110 - a113 + a115 - a117 + a120 - a121 + a125
a107 =(  3*s1 - a108-2*a109 - a112-3*a113 - a114-2*a117 - a118 - 2*a119)/2
a106 =     s1 - a107 - a108 - a109 - a110
a105 =     s1 - a109 - a113 - a117 - a121
a104 =     s1 - a109 - a114 - a119 - a124
a103 =     s1 - a108 - a113 - a118 - a123
a102 =     s1 - a107 - a112 - a117 - a122
a101 =     s1 - a102 - a103 - a104 - a105
a96  =     s1 - a97  - a98  - a99  - a100
a91  =     s1 - a92  - a93  - a94  - a95
a88  =          a89 -2*a93+ 2*a94- 2*a98+2*a99-  a113+ a115-2*a118+2*a120-2*a123+2*a125
a87  =(  5*s1 - a88 -2*a89- 4*a90+   a93-4*a94-2*a95-2*a97- 4*a99- 4*a100-3*a112+  a114-3*a115-2*a117+2*a118+
                                                                                       +2*a119-2*a120+3*a123+2*a124)/3
a86  =     s1 - a87 -  a88 -  a89 -  a90
a85  =(- 4*s1+6*a89-   a90 +3*a92 -9*a93+9*a94-3*a95-3*a97-11*a98 +5*a99- 6*a100+ 2*a108+3*a110-4*a113+4*a114+10*a115+
                                                          - 2*a117-8*a118+2*a119+13*a120+2*a122-5*a123+4*a124+14*a125)/5
a84  =    -s1  +  a85 - a89 + a90-a92 +2*a93 -2*a94 +a95 +  a97+3*a98-a99+2*a100+a113-a115+2*a118-2*a120+2*a123-2*a125
a83  =            a84 + a93 - a94-a108 + a110+  a118-a120
a82  =(  7*s1  +2*a84+2*a87-2*a89-a108-4*a110+3*a112+a113-5*a114-4*a115+4*a117-a118-4*a119-4*a120-2*a122-4*a123+
                                                                                                 -6*a124-8*a125)/2
a81  =     s1  -  a82 - a83 - a84 -  a85
a80  =     s1  -  a84 - a88 - a92 -  a96
a79  =     s1  -  a84 - a89 - a94 -  a99
a78  =     s1  -  a83 - a88 - a93 -  a98
a77  =     s1  -  a82 - a87 - a92 -  a97
a76  =     s1  -  a77 - a78 - a79 -  a80
a75  =(-13*s1/5+2*a76-2*a100+ a108+2*a110+a112-a113+a114+2*a115+  a118+2*a120+2*a122+2*a123+2*a124)/2
a74  =(- 3*s1/5+2*a77-2*a99 + a108+2*a110-a112+a113+a114+2*a115-2*a116-4*a117-  a118+2*a123+4*a125)/2
a73  =   6*s1/5+  a78 - a98 - a108-  a113-a118-   2*a123
a72  =     s1  +  a73 - a97 + a99 +  a113-a114+a117-a119-2*a122-a123-2*a124
a71  =     s1  -  a72 - a73 - a74 -  a75
a70  =(- 3*s1/5+2*a81-2*a95 - a108-2*a110+a112+3*a113+a114+2*a117+a118+2*a119-2*a120)/2
a69  =( 12*s1/5+2*a82-2*a94 - a108-2*a110+a111-a115-a118-4*a119-2*a120+2*a121-2*a125)/2
a68  =     s1/5+  a83 - a93 + a108 - a118
a67  =     s1/5+  a84 - a92 + a110 - a113+a115-2*a117+a120-a121+a125
a66  =     s1  -  a67 - a68 - a69  - a70
a65  =  11*s1/5-  a87-2*a89-2*a90 +2*a93-2*a94+2*a98-2*a99-a112-a114-3*a115+2*a118-2*a120+2*a123-2*a125
a64  =     s1/5+  a87 - a89 + a112 - a114

a63 =   s1/5 a62 = 2*s1/5 - a64 a61 = 2*s1/5 - a65 a60 = 2*s1/5 - a66 a59 = 2*s1/5 - a67 a58 = 2*s1/5 - a68 a57 = 2*s1/5 - a69 a56 = 2*s1/5 - a70 a55 = 2*s1/5 - a71 a54 = 2*s1/5 - a72 a53 = 2*s1/5 - a73 a52 = 2*s1/5 - a74 a51 = 2*s1/5 - a75 a50 = 2*s1/5 - a76 a49 = 2*s1/5 - a77

a48 = 2*s1/5 - a78 a47 = 2*s1/5 - a79 a46 = 2*s1/5 - a80 a45 = 2*s1/5 - a81 a44 = 2*s1/5 - a82 a43 = 2*s1/5 - a83 a42 = 2*s1/5 - a84 a41 = 2*s1/5 - a85 a40 = 2*s1/5 - a86 a39 = 2*s1/5 - a87 a38 = 2*s1/5 - a88 a37 = 2*s1/5 - a89 a36 = 2*s1/5 - a90 a35 = 2*s1/5 - a91 a34 = 2*s1/5 - a92 a33 = 2*s1/5 - a93

a32 = 2*s1/5 - a94 a31 = 2*s1/5 - a95 a30 = 2*s1/5 - a96 a29 = 2*s1/5 - a97 a28 = 2*s1/5 - a98 a27 = 2*s1/5 - a99 a26 = 2*s1/5 - a100 a25 = 2*s1/5 - a101 a24 = 2*s1/5 - a102 a23 = 2*s1/5 - a103 a22 = 2*s1/5 - a104 a21 = 2*s1/5 - a105 a20 = 2*s1/5 - a106 a19 = 2*s1/5 - a107 a18 = 2*s1/5 - a108 a17 = 2*s1/5 - a109

a16 = 2*s1/5 - a110 a15 = 2*s1/5 - a111 a14 = 2*s1/5 - a112 a13 = 2*s1/5 - a113 a12 = 2*s1/5 - a114 a11 = 2*s1/5 - a115 a10 = 2*s1/5 - a116 a9  = 2*s1/5 - a117 a8  = 2*s1/5 - a118 a7  = 2*s1/5 - a119 a6  = 2*s1/5 - a120 a5  = 2*s1/5 - a121 a4  = 2*s1/5 - a122 a3  = 2*s1/5 - a123 a2  = 2*s1/5 - a124 a1  = 2*s1/5 - a125

The linear equations shown above, are ready to be solved, for the magic constant 315.

The solutions can be obtained by guessing:

    a( 89), a( 90), a( 92) ... a( 95), a( 97) ... a(100),
    a(108), a(110), a(112) ... a(115), a(117) ... a(120) and a(122) ... a(125)

and filling out these guesses in the abovementioned equations.

For distinct integers also following relations should be applied:

0 < a(i) =< 125       for i = 1 ... 88, 91, 96, 101 ... 107, 109, 111, 116, 121
a(i) ≠ a(j)           for i ≠ j
Cint(a(i)) = a(i)     for i = 69, 70, 74, 75, 82, 85, 87 and 107

which can be incorporated in a guessing routine which might be used to find other 5^th order Almost Perfect Center Symmetric Cubes.

However, the equations deducted above can be applied in a more efficient way to generate Almost Perfect Center Symmetric Cubes, which will be discussed in Section 5.8.