Magic Cubes (6f)

Office Applications and Entertainment, Magic Cubes
	Index	About the Author

4.7 Analytic Solution Semi Pan Magic Cubes

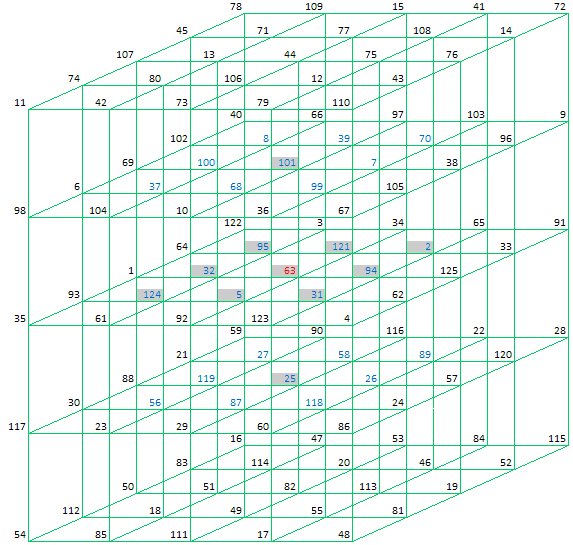
One of the most magic cubes of the 5^th order is the Semi Pan Magic Cube. An example is shown below.

Plane 11 (Top)

78	109	15	41	72
45	71	77	108	14
107	13	44	75	76
74	80	106	12	43
11	42	73	79	110

Plane 12

40	66	97	103	9
102	8	39	70	96
69	100	101	7	38
6	37	68	99	105
98	104	10	36	67

Plane 13

122	3	34	65	91
64	95	121	2	33
1	32	63	94	125
93	124	5	31	62
35	61	92	123	4

Plane 14

59	90	116	22	28
21	27	58	89	120
88	119	25	26	57
30	56	87	118	24
117	23	29	60	86

Plane 15

16	47	53	84	115
83	114	20	46	52
50	51	82	113	19
112	18	49	55	81
54	85	111	17	48

The equations for a Semi Pan Magic Cube of the fifth order can be summarised as follows:

The Rows (25), Columns (25), Pillars (25) and Space Diagonals (4) sum to the Magic Sum (315);
Main - and Pan Diagonals of 2 of the 3 sets of planes sum to the Magic Sum (315);
The equations for Symmetrical Cubes are applicable

In the example shown above the (pan) magic diagonals for the horizontal planes 1.1 thru 1.5 and the vertical planes 3.1 thru 3.5 sum to 315. This is, however, not the case for the vertical planes 2.1 thru 2.5.

Although this depends from the orientation of the cube, this will be used as a guideline in the deduction below.

Plane 11 (Top)

a101	a102	a103	a104	a105
a106	a107	a108	a109	a110
a111	a112	a113	a114	a115
a116	a117	a118	a119	a120
a121	a122	a123	a124	a125

Plane 12

a76	a77	a78	a79	a80
a81	a82	a83	a84	a85
a86	a87	a88	a89	a90
a91	a92	a93	a94	a95
a96	a97	a98	a99	a100

Plane 13

a51	a52	a53	a54	a55
a56	a57	a58	a59	a60
a61	a62	a63	a64	a65
a66	a67	a68	a69	a70
a71	a72	a73	a74	a75

Plane 14

a26	a27	a28	a29	a30
a31	a32	a33	a34	a35
a36	a37	a38	a39	a40
a41	a42	a43	a44	a45
a46	a47	a48	a49	a50

Plane 15

a1	a2	a3	a4	a5
a6	a7	a8	a9	a10
a11	a12	a13	a14	a15
a16	a17	a18	a19	a20
a21	a22	a23	a24	a25

The equations of section 4.2 are applicable with exception of the equations for the plane diagonals of the vertical planes 2.1 thru 2.5.

Further the equations for the pan diagonals of the horizontal planes and the vertical planes 3.1 thru 3.5 have to be added (total 10 * 8 = 80 equations).

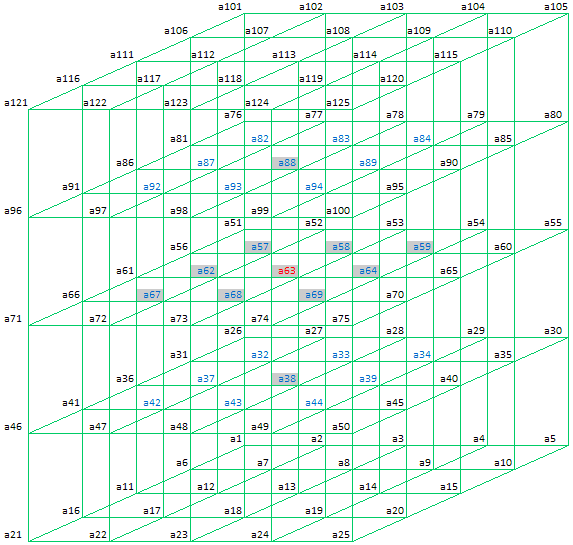
If the equations for symmetric space diagonals are added:

Outer Cube:
a1 + a125 = 126
a5 + a121 = 126

a21 + a105 = 126
a25 + a101 = 126

Inner Cube:
a32 + a94 = 126
a34 + a92 = 126

a42 + a84 = 126
a44 + a82 = 126

following equations, applicable for a Symmetrical Cube, are automatically fulfilled:

Center Pillar:
a13 + a113 = 126

Plane 13:
a51 + a75 = 126
a52 + a74 = 126
a53 + a73 = 126
a54 + a72 = 126
a55 + a71 = 126
a56 + a70 = 126
a60 + a66 = 126
a61 + a65 = 126

Planes 12/14:
a26 + a100 = 126
a27 + a99  = 126
a29 + a97  = 126
a30 + a96  = 126
a31 + a95  = 126
a35 + a91  = 126
a41 + a85  = 126
a45 + a81  = 126
a46 + a80  = 126
a47 + a79  = 126
a49 + a77  = 126
a50 + a76  = 126

Plane 23:
a3   + a123 = 126
a23  + a103 = 126
a78  + a48  = 126
a98  + a28  = 126

Plane 33:
a11  + a115 = 126
a15  + a111 = 126
a36  + a90  = 126
a40  + a86  = 126

Inner Cube:
Center Pillar:
a38 + a88 = 126

Plane 13:
a57 + a69 = 126
a58 + a68 = 126
a59 + a67 = 126
a62 + a64 = 126

Plane 23:
a33 + a93 = 126
a43 + a83 = 126

Plane 33:
a37 + a89 = 126
a39 + a87 = 126

After deduction of the defining equations, the following set of linear equations - describing the Semi Pan Magic Cubes of the 5^th order - can be obtained:

a(121) =  315 - a(122) - a(123) - a(124) - a(125)
a(116) =  315 - a(117) - a(118) - a(119) - a(120)
a(115) =        a(117) + a(118) - a(125)
a(114) =  315 - a(118) - a(119) - a(120) - a(124)
a(113) =  315 - a(117) - a(118) - a(119) - a(123)
a(112) =        a(119) + a(120) - a(122)
a(111) =        a(118) + a(119) - a(121)
a(110) =  315 - a(117) - a(118) - a(122) - a(123)
a(109) = -315 + a(118) + a(119) + a(120) + a(123) + a(124) + a(125)
a(108) = -315 + a(117) + a(118) + a(119) + a(122) + a(123) + a(124)
a(107) =  315 - a(119) - a(120) - a(124) - a(125)
a(106) =  315 - a(118) - a(119) - a(123) - a(124)
a(105) =      - a(120) + a(122) + a(123)
a(104) =  315 - a(119) - a(123) - a(124) - a(125)
a(103) =  315 - a(118) - a(122) - a(123) - a(124)
a(102) =      - a(117) + a(124) + a(125)
a(101) = -315 + a(117) + a(118) + a(119) + a(120) + a(123) + a(124)
a(100) = -441 + a(117) + a(118) + a(119) + a(120) + a(122) + 2 * a(123) + a(124)
a( 99) =  189 - a(117) - a(123)
a( 98) =  504 - a(118) - 2 * a(122) - 2 * a(123) - 2 * a(124)
a( 97) =  189 - a(119) - a(123)
a( 96) = -126 - a(120) + a(122) + 2 * a(123) + a(124)
a( 95) =  189 + a(117) - a(119) - a(123) - a(124)
a( 94) =  504 - a(118) - 2 * a(119) - 2 * a(120) - a(124) - a(125)
a( 93) = -126 + a(122) + a(123) + a(124)
a( 92) = -441 + a(118) + 2 * a(119) + 2 * a(120) + a(123) + a(124) + a(125)
a( 91) =  189 - a(117) + a(119) - a(122) - a(123)
a( 90) = -126 - a(117) + a(119) + a(120) + a(124) + a(125)
a( 89) = -441 + a(118) + 3 * a(119) + 2 * a(120) - a(122) + a(123) + a(124) + a(125)
a( 88) = -126 + a(118) + a(122) + a(124)
a( 87) =  504 + a(117) - a(118) - 2 * a(119) - 2 * a(120) - 2 * a(124) - a(125)
a( 86) =  504 - a(118) - 2 * a(119) - a(120) - a(123) - a(124) - a(125)
a( 85) =  189 - a(119) - 2 * a(120) + a(122) + a(123) - a(125)
a( 84) =  504 + a(117) - a(118) - 2 * a(119) - a(120) - a(123) - 2 * a(124) - a(125)
a( 83) =  504 - a(117) - a(118) - a(119) - a(122) - 2 * a(123) - a(124)
a( 82) = -126 - a(117) + 2 * a(119) + a(120) - a(122) + a(124) + a(125)
a( 81) = -756 + a(117) + 2 * a(118) + 2 * a(119) + 2 * a(120) + a(122) + 2 * a(123) + 2 * a(124) + a(125)
a( 80) =  504 - a(117) - a(118) - 2 * a(122) - 2 * a(123) - a(124)
a( 79) = -441 + a(118) + a(119) + a(120) + a(122) + a(123) + 2 * a(124) + a(125)
a( 78) = -441 + a(117) + a(118) + a(119) + a(122) + 3 * a(123) + a(124)
a( 77) =  189 - a(119) - a(120) + a(122) - a(125)
a( 76) =  504 - a(118) - a(119) - a(122) - 2 * a(123) - 2 * a(124)
a( 75) =  693 - a(118) - a(119) - 2 * a(122) - 3 * a(123) - 2 * a(124) - a(125)
a( 74) =   63 - a(119) - a(120) + a(122) + a(123)
a( 73) = -567 + a(117) + a(118) + a(119) + 2 * a(122) + 3 * a(123) + 2 * a(124)
a( 72) = -252 + a(118) + a(119) + a(120) + a(123) + a(124)
a( 71) =  378 - a(117) - a(118) - a(122) - 2 * a(123) - a(124) + a(125)
a( 70) = -567 + a(118) + 2 * a(119) + a(120) + a(122) + 2 * a(123) + 2 * a(124) + a(125)
a( 69) = -252 - a(117) + a(118) + 2 * a(119) + 2 * a(120) - a(122) + a(124) + a(125)
a( 68) =  378 - a(118) - a(122) - 2 * a(123) - a(124)
a( 67) =  693 - a(118) - 3 * a(119) - 2 * a(120) - a(123) - 2 * a(124) - a(125)
a( 66) =   63 + a(117) - a(119) - a(120) + a(122) + a(123) - a(125)
a( 65) =  378 - a(118) - 2 * a(119) - 2 * a(120) + a(122) - a(124)
a( 64) =  693 + a(117) - a(118) - 3 * a(119) - 2 * a(120) - a(123) - 2 * a(124) - 2 * a(125)

a( 63) = 63
a( 62) = 126 - a(64)
a( 61) = 126 - a(65)
a( 60) = 126 - a(66)
a( 59) = 126 - a(67)
a( 58) = 126 - a(68)
a( 57) = 126 - a(69)
a( 56) = 126 - a(70)
a( 55) = 126 - a(71)
a( 54) = 126 - a(72)
a( 53) = 126 - a(73)
a( 52) = 126 - a(74)
a( 51) = 126 - a(75)
a( 50) = 126 - a(76)
a( 49) = 126 - a(77)

a(48) = 126 - a(78)
a(47) = 126 - a(79)
a(46) = 126 - a(80)
a(45) = 126 - a(81)
a(44) = 126 - a(82)
a(43) = 126 - a(83)
a(42) = 126 - a(84)
a(41) = 126 - a(85)
a(40) = 126 - a(86)
a(39) = 126 - a(87)
a(38) = 126 - a(88)
a(37) = 126 - a(89)
a(36) = 126 - a(90)
a(35) = 126 - a(91)
a(34) = 126 - a(92)
a(33) = 126 - a(93)

a(32) = 126 - a(94)
a(31) = 126 - a(95)
a(30) = 126 - a(96)
a(29) = 126 - a(97)
a(28) = 126 - a(98)
a(27) = 126 - a(99)
a(26) = 126 - a(100)
a(25) = 126 - a(101)
a(24) = 126 - a(102)
a(23) = 126 - a(103)
a(22) = 126 - a(104)
a(21) = 126 - a(105)
a(20) = 126 - a(106)
a(19) = 126 - a(107)
a(18) = 126 - a(108)
a(17) = 126 - a(109)

a(16) = 126 - a(110)
a(15) = 126 - a(111)
a(14) = 126 - a(112)
a(13) = 126 - a(113)
a(12) = 126 - a(114)
a(11) = 126 - a(115)
a(10) = 126 - a(116)
a( 9) = 126 - a(117)
a( 8) = 126 - a(118)
a( 7) = 126 - a(119)
a( 6) = 126 - a(120)
a( 5) = 126 - a(121)
a( 4) = 126 - a(122)
a( 3) = 126 - a(123)
a( 2) = 126 - a(124)
a( 1) = 126 - a(125)

The linear equations shown above, are ready to be solved, for the magic constant 315.

The solutions can be obtained by guessing a(117) ... a(120) and a(122) ... a(125) and filling out these guesses in the abovementioned equations.

For distinct integers also following relations should be applied:

0 < a(i) =< 125 for i = 1 ... 116, 121
a(i) ≠ a(j) for i ≠ j

which have been incorporated in an optimized guessing routine (MgcCube5d).

Subject guessing routine produced - with careful selected sets of the variables a(125) and a(124) (note 47) - Semi Pan Magic Cubes, which are shown in Attachment 4.7.1.

The eight cubes which have been obtained with the 3 Grid Method are shown in Attachment 4.7.2.

A more efficient method to generate Semi Pan Magic Cubes, based on the equations deducted above, will be discussed in Section 5.3.

Index

About the Author

Center Pillar: a13 + a113 = 126	Plane 13: a51 + a75 = 126 a52 + a74 = 126 a53 + a73 = 126 a54 + a72 = 126 a55 + a71 = 126 a56 + a70 = 126 a60 + a66 = 126 a61 + a65 = 126	Planes 12/14: a26 + a100 = 126 a27 + a99 = 126 a29 + a97 = 126 a30 + a96 = 126 a31 + a95 = 126 a35 + a91 = 126 a41 + a85 = 126 a45 + a81 = 126 a46 + a80 = 126 a47 + a79 = 126 a49 + a77 = 126 a50 + a76 = 126	Plane 23: a3 + a123 = 126 a23 + a103 = 126 a78 + a48 = 126 a98 + a28 = 126	Plane 33: a11 + a115 = 126 a15 + a111 = 126 a36 + a90 = 126 a40 + a86 = 126
Inner Cube: Center Pillar: a38 + a88 = 126	Plane 13: a57 + a69 = 126 a58 + a68 = 126 a59 + a67 = 126 a62 + a64 = 126		Plane 23: a33 + a93 = 126 a43 + a83 = 126	Plane 33: a37 + a89 = 126 a39 + a87 = 126